Каган И.Е. О «фазе» и гармонических колебаниях
Каган И.Е. О «фазе» и гармонических колебаниях // Фiзiка: праблемы выкладання. – 2000. – № 3. – С. 57-60.
При изучении гармонических колебаний учащиеся обязательно сталкиваются с понятием «фаза колебаний». Автор приводит несколько определений этого понятия, объясняет физический смысл данной величины.
При изучении гармонических колебаний учащиеся обязательно сталкиваются с понятием «фаза колебаний». В IX классе это понятие не изучается, а в XI классе – часто очень бегло.
Надо заметить еще, что понять смысл гармонического колебания учащимся лучше всего удается в XI классе, потому что они уже знают основы тригонометрии и умеют дифференцировать простейшие функции.
В некоторых учебниках приводится дифференциальное уравнение второго порядка
![]() (1)
(1)
где х – смещение маятника, ω – циклическая частота, ![]() – вторая производная смещения по времени, т.е. ускорение. Решениями этого уравнения являются функции
– вторая производная смещения по времени, т.е. ускорение. Решениями этого уравнения являются функции ![]() или
или
![]() (2)
(2)
т.е. подчеркивается, что гармоническое колебание является синусоидальным или косинусоидальным. Однако в программе средней школы по математике не предусмотрено решение дифференциальных уравнений второго порядка. Как же быть? Думаю, что лучше всего в этом случае с самого начала использовать функцию ![]() или
или ![]() .
.
Если дважды каждую из них продифференцировать по времени, получим исходное дифференциальное уравнение (1).
Учащиеся IX класса не владеют понятием производной и еще не готовы к этой информации. Вот почему в альтернативной программе по физике для 12-летней средней школы раздел «Колебания и волны» вынесен в X класс. Величина
![]() (3)
(3)
является фазой колебания. Проще всего ее определить с точки зрения математики. В некоторых учебниках математики фазой называют все, что стоит под знаком синуса или косинуса.
Однако у фазы имеется и физический смысл.
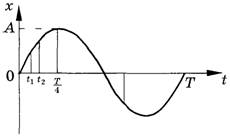
Рис. 1.
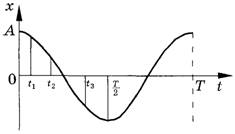
Рис. 2.
Изобразив графики синусоидального или косинусоидального колебаний (рис. 1, 2), можно заметить, что каждому моменту времени соответствует свое развитие колебания. В уравнении (3) фаза φ линейно связана с временем (ведь циклическая частота ωв гармоническом колебании постоянна). Учитывая это, можно дать первоначально смысл фазы как величины, характеризующей момент в развитии колебания. Тогда на горизонтальной оси графиков, изображенных на рис. 3, 4, можно откладывать не только время, но и фазу, учитывая, что продолжительность периода Tзамкнутого цикла по фазе соответствует 2π.
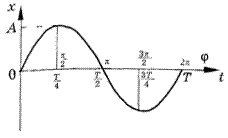
Рис. 3.
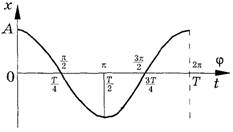
Рис. 4.
Тогда можно сказать о фазе, что это время, выраженное в угловой мере (радианах, градусах), а заодно и в долях периода. Ведь фаза может определять долю периода, прошедшую с момента начала колебания.
Здесь уместно привести пример, показывающий удобство использования понятия «фаза» вместо времени.
Например, никто не сможет сказать, какое смещение будет у маятника в какой-то момент времени, если не известен период колебания. Но всегда можно ответить, какое будет смещение маятника, если известна фаза колебания, не зная, каков по величине период колебания.
Исходя из уравнений (2) или (3), можно дать общее понятие фазы. Фаза ![]() – это величина, функция которой (sin, cos, tg и т.д.) характеризует состояние колебательной системы в любой момент времени. (Физический энциклопедический словарь.)
– это величина, функция которой (sin, cos, tg и т.д.) характеризует состояние колебательной системы в любой момент времени. (Физический энциклопедический словарь.)
Все вышесказанное вполне подходит и для электромагнитных колебаний.
С понятием «фаза» мы сталкиваемся не только в таком упорядоченном периодическом процессе, как колебания. Это понятие применимо к любому процессу и не обязательно к периодическому как определенная часть процесса или определенный момент в развитии того или иного процесса. Все части, на которые разбит тот или иной процесс, можно считать фазами, причем чем мельче раз биение, чем мельче «фазы», тем точнее можно представить ход процесса.
Понятием «фаза» мы пользуемся и в случае «фазовых переходов», т.е. при изменении агрегатного состояния вещества. При этом фаза имеет другой смысл, но и здесь ее можно рассматривать как агрегатное состояние вещества из трех или четырех возможных состояний.
| Выложил | alsak |
| Опубликовано | 27.12.07 |
| Просмотров | 11938 |
| Рубрика | Материалы к уроку |
| Тема | Колебания и волны |