Позойский С.В., Жидкевич В.И. Избранные задачи по теме «Конденсаторные цепи»
Позойский С.В., Жидкевич В.И. Избранные задачи по теме «Конденсаторные цепи» // Фiзiка: праблемы выкладання. – 2006. – № 4. – С. 42-49.
Исправления Сакович А.Л. (ноябрь 2006)
В статье разобраны примеры задач повышенного и углубленного уровня на расчет электрических цепей постоянного тока с конденсаторами. Приводится краткий теоретический материал по данной теме.
Расчет электрических цепей, в которых конденсаторы соединены последовательно или параллельно, производится по известным формулам.
Если в цепи нет участков с последовательно или параллельно соединенными конденсаторами, но есть точки с одинаковыми потенциалами, то их можно либо соединять, либо разъединять, не меняя режима работы цепи. Цепь при этом упрощается, и мы приходим к случаю параллельно и последовательно соединенных конденсаторов.
Если в цепи нет параллельно и последовательно соединенных конденсаторов и нет точек с одинаковыми потенциалами, то для ее расчета используются следующие положения.
1. Сумма зарядов всех обкладок, соединенных с одним из полюсов источника тока, равна заряду источника (закон сохранения заряда):
![]() (1)
(1)
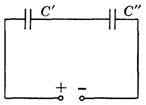
Например, для цепи, изображенной на рисунке 1, ![]() .
.
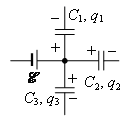
Рис. 1.
2. Если пластины нескольких конденсаторов соединены в один узел, не связанный непосредственно с источником тока, то алгебраическая сумма зарядов на этих пластинах равна нулю (закон сохранения заряда):
![]() (2)
(2)
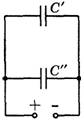
Например, для цепи, представленной на рисунке 2, ![]() .
.
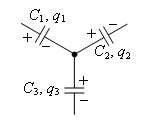
Рис. 2.
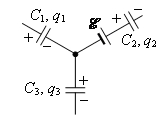
Рис. 3.
Это соотношение справедливо и тогда, когда перед конденсаторами имеются источники ЭДС (рис. 3): ![]() .
.
3. Алгебраическая сумма разностей потенциалов на всех конденсаторах и источниках тока, встречающихся при обходе любого замкнутого контура, равна нулю (закон сохранения энергии):
![]() (3)
(3)
4. Если на каком-либо из участков цепи 1–2 (рис. 4) имеется конденсатор и источник ЭДС, т.е. участок цепи неоднородный, то заряд конденсатора определяется ЭДС источника и разностью потенциалов на концах участка ![]() :
:
![]() (4)
(4)
Если источника ЭДС на участке нет ![]() , то
, то
![]() (5)
(5)
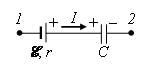
Рис. 4.
Этот факт обусловливает необходимость учитывать выбор знаков в каждом конкретном случае:
а) Если ![]() , т.е. разность потенциалов
, т.е. разность потенциалов ![]() направлена в ту же сторону, что и ЭДС (см. рис. 4), то следует пользоваться формулой (4).
направлена в ту же сторону, что и ЭДС (см. рис. 4), то следует пользоваться формулой (4).
б) Если ![]() , то формулу (4) лучше записать в таком виде:
, то формулу (4) лучше записать в таком виде:
![]() (6)
(6)
где ![]() .
.
В этом случае разность потенциалов «противодействует» ЭДС. Если же при этом ![]() , то для определения заряда формулу (4) следует записать в таком виде:
, то для определения заряда формулу (4) следует записать в таком виде:
![]() (7)
(7)
Правило для определения знаков зарядов на обкладках конденсатора: поле между обкладками конденсатора направлено в ту сторону, в которую направлена сумма ЭДС и разности потенциалов ![]() .
.
В приведенном примере (см. рис. 4) при ![]() и
и ![]() поле конденсатора направлено влево (левая обкладка заряжена отрицательно, правая – положительно);
поле конденсатора направлено влево (левая обкладка заряжена отрицательно, правая – положительно);
Если ![]() , то поле между обкладками конденсатора направлено в сторону меньшего потенциала, т.е. со стороны меньшего потенциала будет обкладка с отрицательным зарядом.
, то поле между обкладками конденсатора направлено в сторону меньшего потенциала, т.е. со стороны меньшего потенциала будет обкладка с отрицательным зарядом.
в) В случае, когда величина потенциалов j1 и j2 неизвестна, следует пользоваться одним из рассмотренных вариантов по своему усмотрению.
Если несколько источников ЭДС и конденсаторов соединены последовательно, то заряд конденсатора определяется из соотношения
![]() (8)
(8)
где ![]() – алгебраическая сумма ЭДС, С – общая емкость конденсаторов.
– алгебраическая сумма ЭДС, С – общая емкость конденсаторов.
![]() (9)
(9)
Правила знаков те же, что и приведенные ранее.
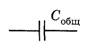
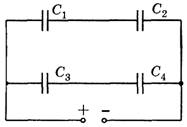
Задача 1. Конденсаторы соединены так, как показано на рисунке 5. Чему равна емкость всей батареи, если емкость каждого конденсатора равна С?
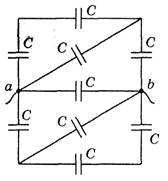
Рис. 5.
Решение. Упростим последовательно цепь (рис. 6).
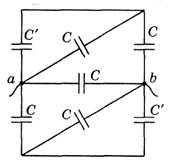
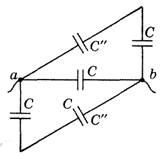
а б
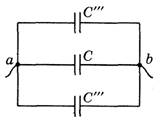
в г
Рис. 6.
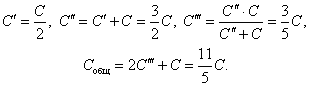
Задача 2. Из проволоки сделан куб, в каждое ребро которого включено по одному конденсатору емкостью С. Найдите емкость батареи (рис. 7).
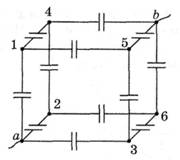
Рис. 7.
Решение. Соединяем точки с одинаковыми потенциалами 1, 2, 3![]() и 4, 5, 6
и 4, 5, 6 ![]() . Получим (рис. 8):
. Получим (рис. 8):
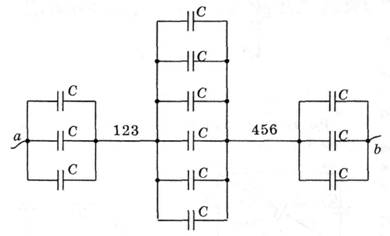
а
![]()
б
Рис. 8.
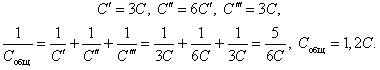
Предлагаем читателю самостоятельно рассмотреть случаи, когда цепь присоединена к источнику тока точками а3 и а6.
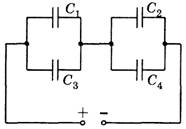
Задача 3. В цепи, изображенной на рисунке 9, С1 = С3 = С; С2 = С4 = С5 = 2С. Найдите емкость батареи конденсаторов.
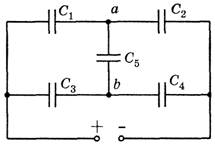
Рис. 9.
Решение. а) Из условия следует, что ![]() , поэтому конденсатор С5 можно «выбросить» (рис. 10, а). Получим:
, поэтому конденсатор С5 можно «выбросить» (рис. 10, а). Получим:
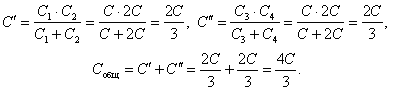
а
 б
б
Рис. 10.
б) Но точки с одинаковыми потенциалами можно также соединить (рис. 11):
![]()
![]()
а
б
Рис. 11.
Задача 4. Определите заряд батареи конденсаторов, изображенной на рисунке 12, если к клеммам АВ приложено напряжение U= 100 B, а емкости конденсаторов C1 = 2 мкФ, С2 = 1 мкФ.
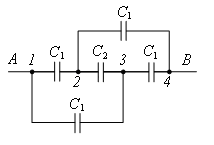
Рис. 12.
Решение. Заменим эту схему эквивалентной (рис. 13, а):
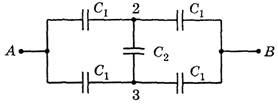
а
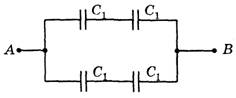 б
б
Рис. 13.
Мы видим, что эта задача аналогична задаче 3. И в этой цепи ![]() и конденсатор С2 можно «выбросить». Тогда получим цепь (рис. 13, б). Общая емкость этой батареи
и конденсатор С2 можно «выбросить». Тогда получим цепь (рис. 13, б). Общая емкость этой батареи ![]() .
.
Находим заряд батареи: ![]() , q = 2∙10–4 Кл.
, q = 2∙10–4 Кл.
Точки 2, 3 можно было и соединить, как в задаче 3. Получили бы тот же результат.
Задача 5. Найдите емкость батареи одинаковых конденсаторов (рис. 14). Емкость отдельного конденсатора С считать известной.
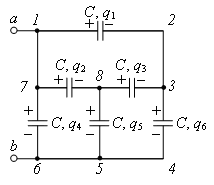
Рис. 14.
Решение. Общая емкость батареи
![]() (1)
(1)
где q – заряд батареи, U – напряжение на ней.
Запишем уравнения для контуров и узлов. Контуры обходим против часовой стрелки. Если при этом мы идем от «–» к «+» на обкладках конденсатора, то соответствующая разность потенциалов берется со знаком «+», если от «+» к «–», то со знаком «–». Выбор направления обхода контура условен: его можно обходить и по часовой стрелке.
Контур 217832:
![]() (2)
(2)
Контур 87658:
![]() (3)
(3)
Контур 38543:
![]() (4)
(4)
Для узла 8:
![]() (5)
(5)
Для узла 3:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Решая эту систему уравнений, получим
![]()
Следовательно, ![]() .
.
Эту же задачу можно решить иначе.
Пусть ![]() .
.
Потенциалы точек 8 и 3 – ![]() .
.
Для определенности будем считать, что ![]() . Тогда
. Тогда
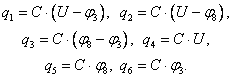
Кроме того, так как ![]() , то
, то
![]() (10)
(10)
![]() (11)
(11)
Из этой системы получим
![]()
Заряд батареи
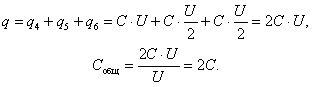
Задача 6. Батарея конденсаторов заряжена до разности потенциалов U0 = 200 В, после чего ее отключили от источника напряжения (рис. 15). Как изменится при этом энергия батареи при замыкании ключа К, если С1 = С2 = С3 = С5 = 1 мкФ; С4 = 0,5 мкФ?
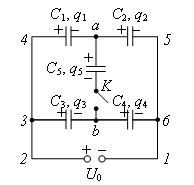
Рис. 15.
Решение. При отключении батареи от источника тока ее заряд не изменится независимо от положения ключа К, а емкость ее после замыкания ключа изменится. Пусть С0, С – емкости батареи до замыкания и после замыкания соответственно, W0, W – соответствующие энергии, q0 = q – заряд батареи.
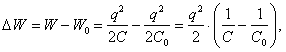 (1)
(1)
где q0 = C0∙U0; q = C∙U; U– напряжение на батарее конденсаторов после замыкания ключа (источник напряжения отключен). До замыкания ключа К
![]() (2)
(2)
Найдем емкость батареи после замыкания ключа.
Узел 3:
![]() (3)
(3)
Узел а:
![]() (4)
(4)
Узел b:
![]() (5)
(5)
Контур а43ba:
![]() (6)
(6)
Контур 5ab65:
![]() (7)
(7)
Контур 5a4215:
![]() (8)
(8)
Из приведенной системы уравнений (1)–(8) находим С0, q, U. Затем из соотношения ![]() определяем С, а из уравнения (1) DW.
определяем С, а из уравнения (1) DW.
Расчеты дают С0 = 0,38 мкФ; Q = 0,85U; С = 0,85 мкФ; DW = –0,39 мДж.
Таким образом, при замыкании ключа энергия батареи уменьшилась. Заметим, что заряд ее не изменился, а емкость увеличилась. Уменьшение энергии обусловлено выделением в цепи теплоты (перераспределение зарядов между конденсаторами сопровождалось возникновением электрического тока в соединительных проводах) и излучением электромагнитных волн при изменении силы тока.
Задача 7. Найдите электродвижущую силу источника тока в схеме, изображенной на рисунке 16. Заряды на конденсаторах 2С и С соответственно 3qи 2q. Внутреннее сопротивление источника не учитывать.
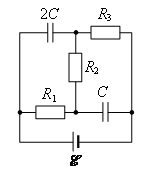
Рис. 16.
Решение. Заряды на обкладках конденсаторов определяются из соотношений:
![]() (1)
(1)
![]() (2)
(2)
где
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
С учетом (3), (4), (5) соотношения (1) и (2) примут вид:
![]() (6)
(6)
![]() (7)
(7)
Делим почленно (1) и (2), получим: ![]() ;
;
![]() (8)
(8)
С учетом (3) и (4) имеем:
![]()
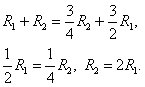 (9)
(9)
Тогда соотношения (6) и (7) примут вид:
![]() (10)
(10)
Проверим результат по (7):
![]() (11)
(11)
Задача 8. Какое количество теплоты выделится в цепи (рис. 17) при размыкании ключа?
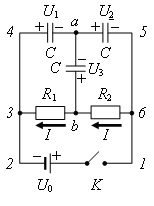
Рис. 17.
Решение. Мы указали на схеме предположительные знаки зарядов на обкладках конденсаторов.
По второму правилу Кирхгофа:
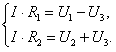 . (1)
. (1)
По закону сохранения заряда ![]() , т.е.
, т.е. ![]() ,
,
![]() (2)
(2)
Решив систему, получим:
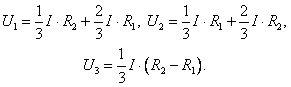
Выделившаяся в цепи теплота
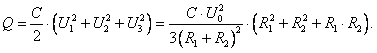 (3)
(3)
Задача 9. В цепи (рис. 18) ![]() = 1 В,
= 1 В, ![]() = 2 В,
= 2 В, ![]() = 3 В, С1 = 20 мкФ, С2 = 30 мкФ, С3 = 60 мкФ. Найдите напряжение на каждом конденсаторе.
= 3 В, С1 = 20 мкФ, С2 = 30 мкФ, С3 = 60 мкФ. Найдите напряжение на каждом конденсаторе.
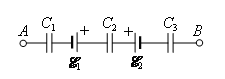
Рис. 18.
Решение. Так как конденсаторы соединены последовательно, то их общая емкость
![]() , C = 10 мкФ.
, C = 10 мкФ.
Следовательно,
![]() , q = 2∙10–5 Кл.
, q = 2∙10–5 Кл.
При последовательном соединении заряды всех конденсаторов одинаковы. Тогда
![]() , U1 = 1 В, U2 =
, U1 = 1 В, U2 = ![]() В, U3 =
В, U3 = ![]() В.
В.
Задача 10. Два конденсатора с емкостями C1 и С2 присоединены к двум источникам с ![]() и
и ![]() (рис. 19). Определите напряжение на каждом конденсаторе и разность потенциалов между точками а и b. Внутреннее сопротивление источников не учитывать.
(рис. 19). Определите напряжение на каждом конденсаторе и разность потенциалов между точками а и b. Внутреннее сопротивление источников не учитывать.
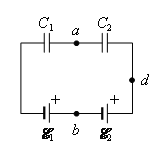
Рис. 19.
Решение. Найдем общую емкость этих двух конденсаторов:
![]() (1)
(1)
Заряды на них одинаковы (конденсаторы соединены последовательно): ![]() .·Заряд на каждом конденсаторе равен заряду на эквивалентной емкости С, т.е.
.·Заряд на каждом конденсаторе равен заряду на эквивалентной емкости С, т.е.
![]() (2)
(2)
Напряжение на конденсаторах:
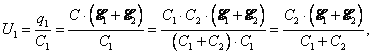 (3)
(3)
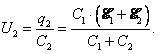 (4)
(4)
Для нахождения Uab рассмотрим участок цепи adb (рис. 20):
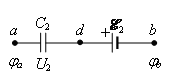
Рис. 20.
Из рисунка видно, что
![]()
Из этих соотношений получаем (вычитая из первого второе):
![]()
Задача 11. Какое количество теплоты выделится в цепи при переключении ключа К из положения 1 в положение 2 (рис. 21)?
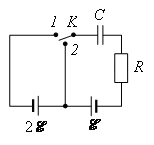
Рис. 21.
Решение. При переключении ключа через батарею ![]() протечет некоторый заряд Dq. Работа батареи равна
протечет некоторый заряд Dq. Работа батареи равна ![]() . Эта работа может частично пойти на увеличение энергии, запасенной в конденсаторе, частично – на выделение теплоты в цепи.
. Эта работа может частично пойти на увеличение энергии, запасенной в конденсаторе, частично – на выделение теплоты в цепи.
Как видно из рис. 21, заряд и, следовательно, энергия, запасенная в конденсаторе, не изменяются при переключении ключа. Меняются лишь знаки зарядов на обкладках. Следовательно, при переключении ключа К через батарею протечет заряд ![]() и в цепи выделится количество теплоты
и в цепи выделится количество теплоты ![]() .
.
Задача 12. Конденсатор емкостью С, заряженный до напряжения U0 = ![]() , подключается через резистор с большим сопротивлением к источнику тока с ЭДС 5
, подключается через резистор с большим сопротивлением к источнику тока с ЭДС 5![]() (рис. 22). Определите количество теплоты, которое выделяется в цепи при зарядке конденсатора до напряжения U = 5
(рис. 22). Определите количество теплоты, которое выделяется в цепи при зарядке конденсатора до напряжения U = 5![]() .
.
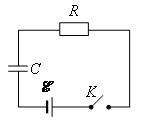
Рис. 22.
Решение. Энергия конденсатора до подключения к источнику тока ![]() . При подключении конденсатора к источнику тока происходит подзарядка его до напряжения 5
. При подключении конденсатора к источнику тока происходит подзарядка его до напряжения 5![]() . При этом через источник тока протечет заряд
. При этом через источник тока протечет заряд ![]() , а энергия конденсатора увеличится и станет равной
, а энергия конденсатора увеличится и станет равной ![]() . Источник совершит работу
. Источник совершит работу ![]() .
.
Часть этой работы затрачивается на увеличение энергии конденсатора, а оставшаяся часть выделится в виде теплоты:
![]()
отсюда
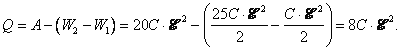
Задача 13. Какое количество теплоты выделится в цепи при переключении ключа К из положения 1 в положение 2 (рис. 23), если емкость каждого конденсатора равна С?
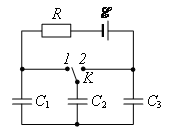
Рис. 23.
Решение. При переключении ключа К емкость цепи не меняется. Напряжение на системе конденсаторов тоже неизменно и равно ![]() . Следовательно, энергия системы не изменяется и вся произведенная батареей работа переходит в теплоту. Для подсчета этой работы необходимо определить заряд, протекший через батарею. До переключения на этом конденсаторе С1 была половина заряда системы, т.е.
. Следовательно, энергия системы не изменяется и вся произведенная батареей работа переходит в теплоту. Для подсчета этой работы необходимо определить заряд, протекший через батарею. До переключения на этом конденсаторе С1 была половина заряда системы, т.е. ![]() (емкость системы равна
(емкость системы равна ![]() ). После переключения заряда на конденсаторе С1 удвоится. Значит, через батарею протечет заряд
). После переключения заряда на конденсаторе С1 удвоится. Значит, через батарею протечет заряд ![]() , и, следовательно, батарея произведет работу
, и, следовательно, батарея произведет работу ![]() . Выделившееся количество теплоты
. Выделившееся количество теплоты ![]() .
.
1. Балаш В.А. Задачи по физике и методы их решения. – М., 1983.
2. Буховцев Б.Б. и др. Сборник задач по элементарной физике. – М., 1987.
3. Гладкова Р.А. Сборник вопросов и задач по физике. – М., 1986.
4. Коган Б.Ю. Задачи по физике. – М., 1971.
5. Савченко Н.Е. Решение задач по физике. – Минск, 1988.
6. Сборник задач по физике / под ред. С.М. Козела. – М., 1990.
| Выложил | alsak |
| Опубликовано | 27.12.07 |
| Просмотров | 77599 |
| Рубрика | Решение задач |
| Тема | Постоянный ток Электростатика |