Акуленко В.Л. Оптимальный угол
Акуленко В.Л. Оптимальный угол // Фiзiка: праблемы выкладання. – 2003. – № 5. – С. 54-64.
В одной из моих публикаций [1] был дан анализ весьма распространенной ошибки в решении задач о наклонной плоскости. Ошибка эта обусловлена тем, что многие авторы пренебрегают частичной потерей кинетической энергии тела при переходе от движения по наклонному участку траектории к участку горизонтальному и наоборот.
К крайнему огорчению, эта ошибка все еще продолжает встречаться, например, в последнем номере нашего журнала [2].
Настораживает и то обстоятельство, что данная ошибка благополучно перешла и в электронные издания, в одном из которых [3] обнаруживаем такую задачу:
«Конькобежец, разогнавшись до скорости υ, въезжает на ледяную горку. На какую высоту Η от начального уровня он поднимется, если горка составляет угол α с горизонтом? Коэффициент трения между коньками и льдом равен k».
Решая эту задачу без учета потери энергии при переходе конькобежца от движения по горизонтальному участку к движению по горке, авторы приходят к следующему ответу:
![]()
Прежде чем анализировать данный результат, хотелось бы отметить, что в большинстве современных изданий, посвященных решению задач по физике, авторы либо не уделяют внимания анализу ответов, либо сводят его к проверке размерности величин, находящихся в левой и правой частях расчетной формулы. В то же время зачастую имеется возможность исследовать простые частные и предельные случаи, ответ для которых очевиден или может быть получен сразу независимо от общего решения.
Такая возможность существует и в нашем случае. Очевидно, что в случае, когда ![]() (т.е. конькобежец сталкивается с практически вертикальной ледяной стеной), о высоте подъема конькобежца речь вести не приходится (Н → 0). Проверим, подтверждается ли данное утверждение полученным авторами ответом.
(т.е. конькобежец сталкивается с практически вертикальной ледяной стеной), о высоте подъема конькобежца речь вести не приходится (Н → 0). Проверим, подтверждается ли данное утверждение полученным авторами ответом.
При ![]()
После такого несложного анализа становится ясно, что приведенное авторами решение является неверным.
Решая данную задачу с учетом потери конькобежцем перпендикулярной к плоскости горки составляющей скорости, получаем следующий ответ:
![]()
При ![]() имеем:
имеем:
![]()
Таким образом, высоту подъема тела в рассмотренной задаче, равно как и длину пробега тела по горизонтальному участку в задачах данного типа с углом наклона плоскости связывает не линейная, а более сложная зависимость. Следовательно, должен существовать тот оптимальный угол наклона плоскости, при котором тело при прочих равных условиях поднимется на максимальную высоту (проделает максимальный путь по горизонтальному участку). Думаю, читателю будут небезынтересны задачи на вычисление этих углов.
Начнем с более простого случая, когда трение на наклонном участке отсутствует.
Задача 1. Под каким углом к горизонтальной площадке следует расположить наклонную плоскость длиной l, чтобы тело, соскользнув с ее вершины, проделало максимально возможный путь s вдоль горизонтального участка? Трение на наклонном участке отсутствует. Коэффициент трения для горизонтального участка ·– μ. Линейными размерами тела пренебречь.
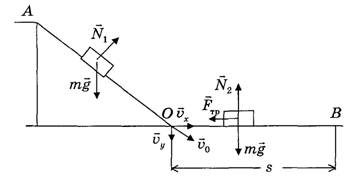
Рис. 1.
Решение. В исходном положении (точка А на рис. 1) тело обладает потенциальной энергией
![]() (1)
(1)
которая по мере движения вдоль наклонной плоскости постепенно превращается в кинетическую энергию. В результате этого в точке О изменения плоскости движения по закону сохранения энергии имеем:
![]() (2)
(2)
где
![]() (3)
(3)
кинетическая энергия тела непосредственно перед ударом о горизонтальную плоскость.
Подставив формулы (1) и (3) в (2), получим:
![]() (4)
(4)
Откуда
![]() (5)
(5)
В процессе удара о горизонтальную плоскость тело потеряет перпендикулярную к ней составляющую ![]() начальной скорости
начальной скорости ![]() и будет осуществлять дальнейшее движение за счет горизонтальной составляющей
и будет осуществлять дальнейшее движение за счет горизонтальной составляющей ![]() .
.
Как видно из рисунка 1,
![]() (6)
(6)
По закону сохранения энергии
![]() (7)
(7)
где
![]() (8)
(8)
![]() (9)
(9)
Подставив выражения (6), (8), (9) в (7), получаем:
![]() (10)
(10)
откуда
![]() (11)
(11)
С учетом равенства
![]() (12)
(12)
получаем
![]() (13)
(13)
Для определения искомого угла наклонаплоскости исследуем на максимум функцию
![]() (14)
(14)
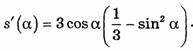 (15)
(15)
Решив уравнение
![]() (16)
(16)
получаем следующие корни:
![]()
(![]() не входит в область определения нашей функции).
не входит в область определения нашей функции).
Точкой максимума нашей функции является ![]()
Ответ: ![]()
Задача 2. Тело соскальзывает с верхнего края доски длиной l и продолжает двигаться вдоль горизонтальной плоскости. Каким должен быть угол α наклона доски, чтобы путь, пройденный телом вдоль горизонтальной плоскости, был наибольшим? Коэффициент трения на всем протяжении пути тела одинаков и равен μ.
Решение. В исходной точке траектории тело обладает потенциальной энергией
![]() (1)
(1)
которая частично превращается в кинетическую энергию
![]() (2)
(2)
а частично расходуется на работу против сил трения на наклонном участке траектории:
![]() (3)
(3)
где Fтpl – сила трения на наклонном участке траектории.По закону сохранения энергии
![]() (4)
(4)
Рассчитаем теперь Атр1, для чего найдем сначала значение силы трения![]() , действующей на тело во время его движения вдоль наклонной плоскости.
, действующей на тело во время его движения вдоль наклонной плоскости.
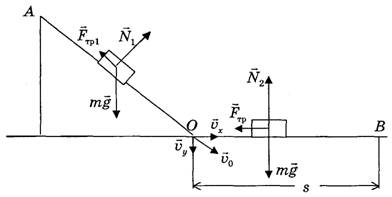
Рис. 2.
По определению
![]() (5)
(5)
где N1 – модуль силы нормальной реакции наклонной плоскости, который, как видно из рисунка 2, определяется выражением
![]() (6)
(6)
Подставив значения выражений (5) и (6) в уравнение (3), получаем:
![]() (7)
(7)
После подстановки значений (1), (2) и (3) в уравнение (4), получаем:
![]() (8)
(8)
Решив уравнение (8) относительно υ1, имеем:
![]() (9)
(9)
Дальнейшее решение, аналогичное решению задачи 1, приводит нас к результату:
![]() (10)
(10)
Отметим, что данный ответ справедлив при условии
![]() (11)
(11)
(в противном случае тело просто не сдвинется с места). Исследовав на максимум функцию
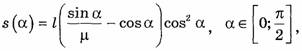
получаем значение угла наклона плоскости, обеспечивающего максимальное значение s:
![]()
Ответ: ![]()
Как следует из полученного ответа, значение угла α в рассматриваемом случае зависит от коэффициента трения μ. Рассчитаем углы α1 и α2, соответствующие наиболее часто встречающимся в школьном курсе физики значениям коэффициента трения:
![]()
![]()
Предлагаю читателю для самостоятельного решения задачу 3.
Камень бросают под некоторым углом α к горизонту с начальной скоростью υ0. Приземлившись, он продолжает движение, скользя по твердой горизонтальной площадке с коэффициентом трения μ. Определите значение угла между вектором скорости ![]() и горизонталью, при котором перемещение камня будет наибольшим. Сопротивление воздуха не учитывать.
и горизонталью, при котором перемещение камня будет наибольшим. Сопротивление воздуха не учитывать.
Ответ: ![]()
Приложение 1. Исследование на максимум функций:
1) 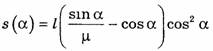 (задача 2);
(задача 2);
2) ![]() (задача 3).
(задача 3).
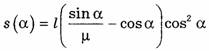 в области определения
в области определения ![]()
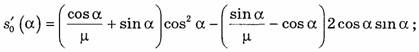
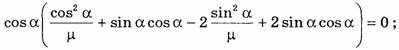
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Нашим условиям отвечает только положительноезначение:
![]()
![]()
![]()
2) Исследуем на максимум функцию ![]()
![]() на промежутке
на промежутке ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Приложение 2(решение задачи 3).
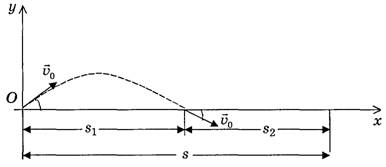
Рис.3.
Решение. Как видно из рисунка 3, модуль перемещения камня состоит из двух частей – перемещения, совершенного камнем в полете (s1), и перемещения, совершенного в результате скольжения тела (s2), т.е.
![]() (1)
(1)
![]() (2)
(2)
где
![]() (3)
(3)
время полета камня. Подставив значение (3) в уравнение (2), получаем:
![]() (4)
(4)
Скользить вдоль горизонтального участка камень начнет со скоростью
![]() (5)
(5)
которой соответствует кинетическая энергия
![]() (6)
(6)
По закону сохранения энергии:
![]() (7)
(7)
где Aтр – работа против сил трения, определяемая выражением:
![]() (8)
(8)
Подставив значения (6) и (8) в (7) и решив полученное уравнение относительно s2, получаем:
![]() (9)
(9)
После подстановки выражений (4) и (9) в(1) получим:
![]() (10)
(10)
Исследовав на максимум функцию
![]()
получаем:
![]()
Ответ: ![]()
1. Акуленко В.Л. Классическая ошибка // Фiзiка: праблемы выкладання. – 2002. – № 3.
2. Редькин В.П., Николаенко Т.В., Дуб Н.Н. Задачи по физике. Методы решения // Фiзiка: праблемы выкладання. – 2003. – № 1.
3. Мультимедийный самоучитель по физике на CD-ROM «TeachPro Физика Механика».
| Выложил | alsak |
| Опубликовано | 12.07.07 |
| Просмотров | 15890 |
| Рубрика | Решение задач |
| Тема | Кинематика Законы сохранения Динамика |