Дешковский А., Койфман Ю.Г. Метод размерностей в решении задач
Дешковский А., Койфман Ю. Метод размерностей в решении задач //ФПВ. – 2002. – № 2. – С. 71-81.
При решении задач по физике на любом уровне необычайно важно определить наиболее приемлемый метод или методы, а уж затем перейти к «техническому» воплощению. Учителя-виртуозы (мы сознательно употребили это выражение, так как считаем во многом схожим прочтение музыкального произведения музыкантами-импровизаторами и учителями-виртуозами, нашедшими собственные, авторские подходы в трактовке и толковании физических закономерностей) уделяют много времени предварительному обсуждению проблемы. Говоря другими словами, обсуждение метода зачастую не менее важно, чем решение задачи, поскольку происходит своеобразный обмен методиками, соприкосновение различных точек зрения, что, собственно, и является целью процесса обучения. Процесс подготовки к решению задачи во многом напоминает процесс подготовки актера к спектаклю. Обсуждение ролей, характеров героев, обдумывание интонаций, музыкальных реприз и художественных декораций являются важнейшими элементами погружения актера в роль. Не случайно, что многие известные театральные работники ценят подготовительный процесс и вспоминают атмосферу репетиций и собственные находки. В процессе преподавания учитель использует различные методы или «спектр методов». Одним из общих методов решения является решение задач методом размерности. Суть данного метода заключается в том, что искомая закономерность может быть представлена в виде произведения степенных функций физических величин, от которых зависит искомая характеристика. Важным моментом в решении является нахождение этих величин. Анализ размерностей левой и правой частей соотношения позволяет определить аналитическую зависимость с точностью до постоянного множителя.
![]() (1)
(1)
Здесь p– давление газа, т0 – масса молекулы, n – концентрация, u – скорость молекулы.
![]()
Зависимость (1) на языке размерностей имеет вид:
![]() (2)
(2)
![]() (3)
(3)
Сравнение размерности левой и правой части дает систему уравнений
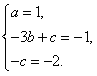 (4)
(4)
![]() (5)
(5)
Обратим внимание на то, что коэффициент пропорциональности нельзя определить, используя метод размерностей, но, тем не менее, мы получили неплохое приближение к известному соотношению (основное уравнение мо-лекулярно-кинетической теории).
Рассмотрим несколько задач, на примере решения которых продемонстрируем суть метода размерностей.
![]() (6)
(6)
Представим все вышеупомянутые величины:
![]() (7)
(7)
С учетом (7) перепишем искомую закономерность выражением
![]() (8)
(8)
![]() (9)
(9)
Теперь уже нетрудно записать систему уравнений:
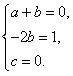 (10)
(10)
![]() (11)
(11)
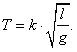 (12)
(12)
Задача 2. Эксперименты показали, что скорость звука в газах зависит от давления и плотности среды. Сравните скорости звука в газе для двух состояний ![]() .
.
На первый взгляд кажется, что нам необходимо ввести в рассмотрение температуру газа, так как хорошо известно, что скорость звука зависит от температуры. Однако (сравните с рассуждением выше) давление может быть выражено как функция плотности (концентрации) и температуры среды. Поэтому одна из величин (давление, плотность, температура) является «лишней». Поскольку по условию задачи нам предлагается сравнить скорости разных давлений и плотностей, то разумно исключить из рассмотрения температуру. Отметим, что если бы нам надо было сделать сравнение для разных давлений и температур, то мы бы исключили плотность.
![]() (13)
(13)
![]()
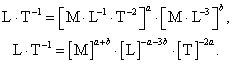 (14)
(14)
Из (14) имеем
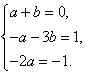 (15)
(15)
Решение (15) дает ![]() .
.
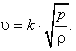 (16)
(16)
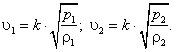 (17)
(17)
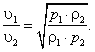 (18)
(18)
Задача 3. На цилиндрический столб намотан канат. За один из концов каната тянут с силой F. Для того чтобы канат не скользил по столбу, когда на столб намотан лишь один виток, второй конец удерживается с силой f. С какой силой нужно удерживать этот конец каната, если на столб намотано n витков? Как изменится сила f, если выбрать столб вдвое большего радиуса? (Сила f не зависит от толщины каната.)
![]() (19)
(19)
![]() (20)
(20)
так как а = 1; с = 0 (a – коэффициент пропорциональности, связанный с μ). Для второго, третьего, ..., п-го намотанного витка запишем аналогичные выражения:
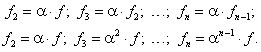 (21)
(21)
![]() (22)
(22)
Хорошо известно, что «метод размерностей» зачастую с успехом применяется в гидродинамике и аэродинамике. В некоторых случаях он позволяет «оценить решение» достаточно быстро и с хорошей степенью надежности.
Задача 4. Оцените силу сопротивления тел, движущихся в жидкости.
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
где ![]() . Коэффициент с характеризует обтекаемость тел и принимает различные значения для тел: для шара с = 0,2 – 0,4, для круглого диска с = 1,1 – 1,2, для каплеобразного тела с » 0,04. (Яворский Б.М., Пинский А.А. Основы физики. – Т. 1. – М.: Наука, 1974.)
. Коэффициент с характеризует обтекаемость тел и принимает различные значения для тел: для шара с = 0,2 – 0,4, для круглого диска с = 1,1 – 1,2, для каплеобразного тела с » 0,04. (Яворский Б.М., Пинский А.А. Основы физики. – Т. 1. – М.: Наука, 1974.)
До сих пор мы рассматривали примеры, в которых коэффициент пропорциональности оставался безразмерной величиной, однако это не означает, что мы должны всегда следовать этому. Вполне возможно сделать коэффициент пропорциональности «размерным», зависящим от размера основных величин. Например, вполне уместно представить гравитационную постоянную ![]() . Говоря другими словами, наличие размерности у гравитационной постоянной означает, что ее численное значение зависит от выбора основных величин. (Здесь нам кажется уместным сделать ссылку на статью Д.В.Сивухина «О международной системе физических величин», УФН, 129, 335, 1975.)
. Говоря другими словами, наличие размерности у гравитационной постоянной означает, что ее численное значение зависит от выбора основных величин. (Здесь нам кажется уместным сделать ссылку на статью Д.В.Сивухина «О международной системе физических величин», УФН, 129, 335, 1975.)
Задача 5. Определите энергию гравитационного взаимодействия двух точечных масс т1 и т2, находящихся на расстоянии r друг от друга.
![]() (26)
(26)
![]() (27)
(27)
Анализируя соотношение (26), найдем, что
а = 1; b = 1; с = –1,
![]() (28)
(28)
Задача 6. Найдите силу взаимодействия между двумя точечными зарядами q1 и q2, находящимися на расстоянии r.
![]() (29)
(29)
![]() (30)
(30)
Проделав все преобразования, получим систему уравнений
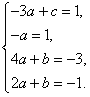 (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
В соотношении (33) отсутствует безразмерный коэффициент 4π, который был введен по историческим причинам.
Задача 7. Определите напряженность гравитационного поля бесконечного цилиндра радиусом r0 и плотностью r на расстоянии R (R > r0) от оси цилиндра.
![]()
![]() (34)
(34)
![]() (35)
(35)
Составим систему уравнений:
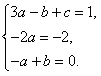 (36)
(36)
![]() (37)
(37)
Отметим, что замена переменной позволила упростить решение задачи.
Решить же предложенную задачу методом размерностей без замены переменной весьма сложно.
Рассмотрим задачу, которую можно решить, применяя принцип разбиения «одинаковой» размерности на «разные».
Задача 8. Оцените дальность полета и высоту тела, брошенного под углом a к горизонту. Сопротивлением воздуха пренебречь.
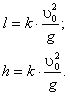 . (38)
. (38)
![]()
![]()
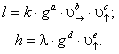 (39)
(39)
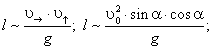 (40)
(40)
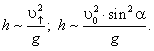 (41)
(41)
Данный метод является более сложным, однако хорошо работает, если имеется возможность различить величины, измеряемые одной и той же единицей измерения. Например: инерционная и гравитационная масса («инерционные» и «гравитационные» килограммы), вертикальное и горизонтальное расстояние («вертикальные» и «горизонтальные» метры), сила тока в одной и другой цепи и т.п.
Суммируя все вышеизложенное, отметим:
1. Метод размерностей может быть использован в случае, если искомая величина может быть представлена в виде степенной функции.
2. Метод размерностей позволяет качественно решить задачу и получить ответ с точностью до коэффициента.
3. В некоторых случаях метод размерностей является единственным способом решить задачу и хотя бы оценить ответ.
4. Анализ размерностей при решении задач широко используется в научных исследованиях.
5. Решение задач методом размерностей является дополнительным или вспомогательным методом, позволяющим лучше понять взаимодействие величин, их влияние друг на друга.
| Выложил | alsak |
| Опубликовано | 03.01.08 |
| Просмотров | 26190 |
| Рубрика | Решение задач |
| Тема | Без тем |