Акуленко В.Л. Некоторые аспекты изучения закона сохранения импульса в школьном курсе физики
Акуленко В. Л. Некоторые аспекты изучения закона сохранения импульса в школьном курсе физики // Фiзiка: праблемы выкладання. – 2009. – № 3. – С. 21–24.
Процессы запоминания, осознанного восприятия (понимания) и повторения физических законов, происходящего в ходе их применения, являются взаимосвязанными и взаимовлияющими. Запоминание большинства физических законов основано на сохранении в памяти выражающей тот или иной закон формулы, поскольку формула в отличие от формулировки подлежит зрительному восприятию и объём находящейся в ней информации не превышает максимального объёма кратковременной памяти. Прочное усвоение любого учебного материала (в том числе и физических законов), перевод его из кратковременной памяти в долговременную обеспечивается работой, направленной на углубление понимания этого материала, а также его регулярным повторением.
Формулировка физического закона чаще всего строится на основе соответствующей формулы, и в ряде случаев это даёт положительный результат (второй закон Ньютона, закон всемирного тяготения, закон Ома и т.д.).
Совсем по-другому дело обстоит с законом сохранения импульса. Воспроизводя его, учащиеся чаще всего говорят о равенстве импульсов тел системы до взаимодействия и после взаимодействия, упуская из виду то обстоятельство, что импульс сохраняется и во время взаимодействия.
Попытаемся разобраться с причиной этого явления. Во-первых, в школьных учебниках и ряде других учебных пособий при выводе закона сохранения импульса действительно рассматривают импульсы тел, входящих в замкнутую систему, до взаимодействия и после взаимодействия. В результате в памяти учащегося откладывается информация следующего вида: "Если в замкнутой системе п тел и их импульсы до взаимодействия —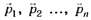 , после взаимодействия —
, после взаимодействия — 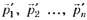 , то
, то
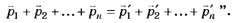
Абсолютно же верная и корректная формулировка закона сохранения импульса, имеющаяся в тех же учебниках, — "Векторная сумма импульсов всех тел, входящих в систему, остаётся неизменной при любых движениях и взаимодействиях тел системы" — остаётся где-то на "задворках памяти".
Во-вторых, предлагаемые в школьном учебнике задачи, иллюстрирующие закон сохранения импульса, не способствуют его глубокому пониманию: в процессе их решения по-прежнему сравниваются импульсы тел, входящих в систему до и после взаимодействия.
И, наконец, в ряде пособий авторы дают алгоритм решения задач на закон сохранения импульса, одним из пунктов которого является предписание сравнить сумму импульсов тел, входящих в замкнутую систему, до взаимодействия и после взаимодействия.
В результате у многих школьников не сформировано понимание закона сохранения импульса во всей полноте. Оперируя по сути дела "законом равенства импульсов тел до и после взаимодействия", они остаются бессильными перед задачами, в ходе решения которых необходимо рассматривать импульс системы в определённый момент взаимодействия.
Выход из данной ситуации только один — через решение соответствующих задач. Предлагаю вниманию читателей одну из них.
Задача 1. Происходит соударение двух абсолютно упругих шаров, массы которых равны m1 и m2. Начальные скорости шаров равны v1и v2 - удар центральный. Определите максимальную энергию упругой деформации.
Решение. Энергия упругой деформации шаров станет максимальной в тот момент времени, когда станет равной нулю их относительная скорость, или, что одно и то же, станут равными друг другу их абсолютные скорости. Запишем для этого момента времени закон сохранения механической энергии и закон сохранения импульса:
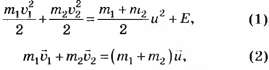
где 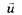 — скорость обоих шаров в рассматриваемый момент времени, Е — искомая энергия.
— скорость обоих шаров в рассматриваемый момент времени, Е — искомая энергия.
Поскольку в условии задачи не указано, как движутся шары — в одну сторону или навстречу друг другу, рассмотрим оба случая.
В первом случае (шары движутся в одну сторону) проекция уравнения (2) будет иметь вид:
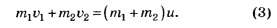
Во втором случае (шары движутся навстречу друг другу) проекция уравнения (2) примет вид:
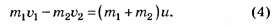
Решив системы уравнений (1) и (3) для первого случая и (1) и (4) для второго случая, найдём соответствующие значения максимальной энергии упругой деформации:
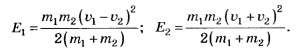
Анализ ответа. Выделим частный случай, в котором
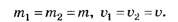
Получим ответ к задаче с данными условиями для первого случая. Поскольку шары движутся в одном направлении с одинаковыми скоростями, соударения между ними не произойдёт, а значит, максимальная энергия упругой деформации Е1 будет равна нулю.
Во втором случае происходит соударение двух шаров, имеющих одинаковые массы и равные по модулю скорости. Следовательно, в определённый момент произойдёт остановка шаров. Именно в этот момент времени и станет максимальной энергия упругой деформации (вся кинетическая энергия шаров перейдёт в энергию упругой деформации), т.е.
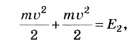
или
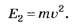
Таким образом, при m1= m2= m, v1= v2= v получаем ответы:
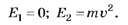
Проверим, предусматривают ли общие формулы ответов рассмотренный выше частный случай.
При m1= m2= m, v1= v2= v:
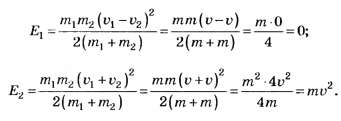
Предлагаю читателям для самостоятельного решения ещё две задачи.
Задача 2. На гладкой горизонтальной поверхности расположен брусок массой m, к одной из сторон которого прикреплена лёгкая пружина жёсткостью k (рис. 1). Другой брусок массой m0 , движущийся по этой же поверхности со скоростью v0 , налетает
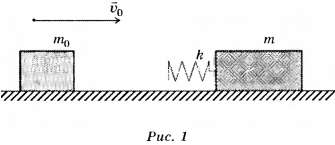
на покоящийся брусок со стороны пружины. Найдите максимальную деформацию пружины.
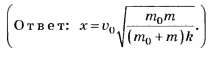
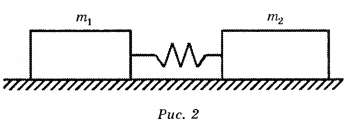
Задача 3. Два бруска массами m1 = 450г и m2 = 800 г, прикреплённые к концам невесомой пружины (рис. 2), удерживают на гладкой горизонтальной поверхности так, что пружина сжата, причём её абсолютное удлинение 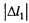 . Сначала отпускают только брусок массой m1, а в тот момент, когда пружина не деформирована, отпускают второй брусок. Если максимальное значение абсолютного удлинения пружины в процессе дальнейшего движения брусков
. Сначала отпускают только брусок массой m1, а в тот момент, когда пружина не деформирована, отпускают второй брусок. Если максимальное значение абсолютного удлинения пружины в процессе дальнейшего движения брусков 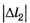 = 8,0 см то
= 8,0 см то 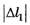 было равно ... см.
было равно ... см.
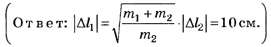
Список использованной литературы
1. Исиченкова, Л. А. Физика: учеб. пособие для 9 кл. общеобразоват. шк. с рус. яз. обучения / JI. А. Исаченкова, И. И. Жолнеревич, И. Н. Медведь. — Минск : Нар. асвета, 2000. — 214 с.
2. Жолнеревич, И. И. Физика: учеб. пособие для 10 кл. учреждений, обеспечивающих получение общ. сред, образования, с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) / И. И. Жолнеревич, И. Н. Медведь. — 2-е изд. — Минск: Нар. асвета, 2007. — 263 с.
3. Буховцев, Б. Б. Сборник задач по элементарной физике: пособие для самообразования / Б. Б. Буховцев [и др.]. — М. : Наука, 1987. — 416 с.
4. Кравцова, В. Н. Законы сохранения в механике: учеб.-метод. пособие / В. Н. Кравцова; Академия последипломного образования. — Минск : АПО, 2006. — 62 с.
5. Централизованное тестирование. Физика: сборник тестов / Респ. ин-т контроля знаний М-ва образования Респ. Беларусь. — Минск: Аверсэв, 2008. — 94 с.
6. Слободянюк, А. И. Физика для "зубров" /А. И. Слободянюк, Л. Г. Маркович. — Минск : Белорус, ассоц. "Конкурс", 2007. — 160 с.
| Выложил | alsak |
| Опубликовано | 28.02.12 |
| Просмотров | 7619 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |