Кротов В.М. О размерностях физических величин
Кротов В.М. О размерностях физических величин // Фiзiка: праблемы выкладання. – 1997. – № 9. – С. 87-91.
Часто неправильно трактуется понятие о размерности физических величин: взаимозаменяются понятия единицы измерения и размерности физических величин. Поэтому и видится необходимым еще раз описать содержание этого понятия и указать возможности его использования в процессе обучения физике.
Метрология – составная часть школьного курса физики. Основные ее понятия: физическая величина, значение физической величины, система физических величин, основная физическая величина, производная физическая величина, дополнительная физическая величина, уравнение связи между физическими величинами. Названные понятия находятся в определенной взаимосвязи и взаимоотношениях, которые, к сожалению, не всегда точно отражаются при организации познавательной деятельности учащихся. Наиболее часто неправильно трактуется понятие о размерности физических величин: взаимозаменяются понятия единицы измерения и размерности физических величин. Поэтому и видится необходимым еще раз описать содержание этого понятия и указать возможности его использования в процессе обучения физике.
Размерность физической величины – одна из важнейших ее характеристик, которую можно определить как буквенное выражение, отражающее связь данной величины с величинами, принятыми за основные в рассматриваемой системе величин. Так, система величин, которая именуется Международной системой единиц, содержит семь основных системных величин: l, m, t, Ι, Τ, n и J, где l– длина, m – масса, t – время, I – сила электрического тока, Τ – термодинамическая температура, ν – количество вещества, J – сила света. Для этих величин условно приняты следующие размерности: для длины – L, массы – М, времени – Т, силы электрического тока – I, термодинамической температуры – Θ, количества вещества – N и силы света – J. Размерности записывают прописными буквами и печатают прямым шрифтом [4].
Размерность величины x обозначается через ![]() . Например:
. Например: ![]() . Над размерностями величин, как и над самими величинами, можно производить действия умножения, деления, возведения в степень и извлечения корня. Показатель степени, в которую возведена размерность основной величины, входящей в степенной одночлен, называют показателем размерности [4; 5].
. Над размерностями величин, как и над самими величинами, можно производить действия умножения, деления, возведения в степень и извлечения корня. Показатель степени, в которую возведена размерность основной величины, входящей в степенной одночлен, называют показателем размерности [4; 5].
Размерность производных физических величин определяется исходя из уравнения связи между физическими величинами. Например,
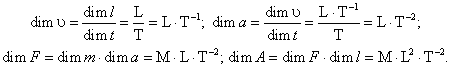
Различают как размерные, так и безразмерные физические величины. К первым относят такие величины, в размерностях которых хотя бы один из показателей размерности не равен нулю. Безразмерными физическими величинами называют физические величины, в размерностях которых все показатели размерности равны нулю.
По поводу физического смысла размерностей физических величин существуют различные взгляды. М.Планк писал: «Ясно, что размерность какой-либо физической величины не есть свойство, связанное с существом ее, но представляет просто некоторую условность, определяемую выбором системы измерений» [3, 72]. Другой точки зрения придерживался известный ученый А.Зоммерфельд. Он связывал выбор основных физических величин и их размерностей с самой сущностью физических величин [3].
Важно знание не столько размерностей физических величин, сколько использование их для освоения физических знаний. В этой связи интересным является тот факт, что во многих областях физики и смежных науках применяется метод исследования, который получил название анализа размерностей. Особенно плодотворным он оказывается в тех случаях, когда нахождение искомой закономерности прямым путем либо встречает значительные математические трудности, либо требует знания таких деталей, которые заранее неизвестны» [3, 79],
Применение метода анализа размерностей началось со времени И.Ньютона. Его развивали и уточняли У.Томсон, Дж.Рэлей. Э.Ферми утверждал, что действительно понимающие природу того или иного явления должны уметь получать основные закономерности из соображений размерностей.
В процессе обучения физике в средней школе метод анализа размерностей качественно без сложных математических выводов позволяет:
1) получать выражения физических законов,
2) определять физический смысл используемых соотношений,
3) проверять правильность записи формул,
4) решать задачи,
5) обнаруживать ошибки в их решении [1; 2].
Хотя полученные с его применением результаты всегда содержат некоторую неопределенность (зависимости устанавливаются с точностью до постоянных коэффициентов), однако при этом повышается осознанность и научность освоения физических знаний.
Осознанное использование метода анализа размерностей станет возможным при освоении учащимися алгоритма его применения. Рассмотрим основные этапы реализации данного метода на примере установления зависимости емкостного сопротивления в цепи переменного тока от частоты переменного тока и электроемкости конденсатора:
1. Экспериментальное установление зависимости сопротивления конденсатора, включенного в цепь переменного тока, от частоты переменного тока и электроемкости конденсатора.
2. Запись уравнения связи между названными величинами в общем виде ![]() , где Ζ – безразмерный коэффициент.
, где Ζ – безразмерный коэффициент.
3. Запись размерностей величин, входящих в уравнение связи
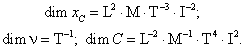
4. Подстановка размерностей величин в уравнение связи
или
5. Составление системы уравнений
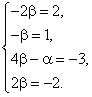
6. Решение полученных систем уравнений
β = –1, –4 – α = –3, α = –1.
7. Подстановка значений α и β в уравнение связи
Таким образом, конденсатор в цепи переменного тока обладает сопротивлением, которое обратно пропорционально частоте переменного тока ν и электроемкости конденсатора С.
8. Определение значения коэффициента Ζ (может быть экспериментальным)
9. Запись окончательной формулы
Таким же способом можно примените метод анализа размерностей для установления многих других закономерностей и законов, например:
1) формула для определения периода колебаний груза на пружине;
2) формула для определения периода колебаний математического маятника;
3) основное уравнение МКТ;
4) формула для определения силы Лоренца;
5) зависимость индуктивного сопротивления от частоты переменного тока и индуктивности катушки;
6) формула Томсона;
7) формула для определения потенциала поля, созданного точечным зарядом.
Применение метода анализа размерностей к решению задач более сложно. Примеры решения задач рассматриваемым методом описаны в литературе [3]. Не вызывает затруднений применение метода анализа размерностей к проверке правильности вывода рабочих формул, для этого в уравнение связи между физическими величинами подставляются их размерности. При равенстве показателей размерностей в обеих частях равенства можно утверждать, что формула выведена правильно.
Опыт реализации метода размерностей в практику обучения учащихся показывает [2], что понятие о размерностях физических величин можно вводить в IX классе по ныне действующим программам. Для этого наряду с установлением единиц измерения физических величин определяются и их размерности. Размерности всех изучаемых величин заносятся в специальную таблицу, которой учащиеся пользуются при определении закономерностей, решении задач, установлении размерностей вновь вводимых физических величин.
1. Голин Г.М., Истаров В.В. Использование метода размерностей в школьной физике // Физика в школе. – 1990. – № 2. – С. 36-40.
2. Кротов В.М. Метод анализа размерностей при обучении физике учащихся педагогических классов // Даiнстытуцкая падрыхтоўка моладзi i арыентацыя яе на педагагiчныя прафесii, вопыт i праблемы (Матэрыялы рэспублшанскай канферэнцыi). – Минск, 1992. – С. 102-103.
3. Сена Л.А. Единицы физических величин и их размерности. – М.: Наука, 1977. – 335 с.
4. Стоцкий JI.P. Физические величины и их единицы. – М.: Просвещение, 1984. – 239 с.
5. Чертов А.Г. Международная система единиц измерения. – М.: Высшая школа, 1967.
| Выложил | alsak |
| Опубликовано | 26.12.07 |
| Просмотров | 15614 |
| Рубрика | Решение задач |
| Тема | Без тем |