Баканина Л.П. Законы Ньютона //Квант
Баканина Л. Законы Ньютона //Квант. — 1982. — №12. — С. 38-41.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Основные законы динамики были установлены около трехсот лет тому назад великим английским ученым Исааком Ньютоном (1643-1727). Ньютон сформулировал их следующим образом (А. Г. Дорфман. «Всемирная история физики». М., «Наука», 1974):
Закон I. Всякое тело продолжает сохранять свое состояние покоя или равномерного прямолинейного движения, поскольку оно не принуждается приложенными силами изменять это состояние.
Закон II. Изменение (количества) движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Закон III. Действие всегда встречает равное противодействие, или воздействия двух тел друг на друга между собой равны и направлены в противоположные стороны.
За 300 лет эти законы многократно подвергались экспериментальной проверке, и никаких нарушений обнаружено не было. Уточнялись лишь границы их применимости и вносились поправки, необходимые для областей микромира и скоростей, близких к скорости света.
Очевидно, что первый закон, по существу, постулирует существование таких систем отсчета (связанных с материальными объектами), в которых справедливы второй и третий законы Ньютона. Эти системы отсчета называют инерциальными.
Третий закон утверждает, что сила всегда является результатом взаимодействия двух каких-то тел. Если рассмотреть все тела, которые взаимодействуют с исследуемым телом, можно определить все силы, на него действующие. В современной физике силы взаимодействия делят на четыре больших класса: гравитационные, электромагнитные, сильные и слабые (два последних класса относятся к ядерным взаимодействиям). В механике, кроме гравитационных сил, принято выделять силы упругости и силы трения. По происхождению две последние силы — электромагнитные, но каждая из них имеет свои особенности и потому рассматривается отдельно.
Основным является, конечно, второй закон, который в настоящее время чаще всего записывается в виде
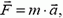
где 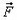 — действующая на тело сила, m — масса тела и
— действующая на тело сила, m — масса тела и 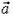 — приобретаемое телом ускорение. Если известны все действующие силы, с помощью этого закона можно найти ускорение тела, а, следовательно, скорость и координаты в любой момент времени.
— приобретаемое телом ускорение. Если известны все действующие силы, с помощью этого закона можно найти ускорение тела, а, следовательно, скорость и координаты в любой момент времени.
Поясним сказанное на конкретных задачах . Большинство из них предлагалось на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Сила, действующая на тело, периодически меняет свое направление на противоположное (рис. 1, а). Как движется тело под действием такой силы?
Рассмотрим, как зависят от времени скорость тела и его перемещение вдоль линии действия силы (пусть это будет ось X). Для определенности будем считать, что начальные скорость и координата равны нулю.
На участке 0-1 сила постоянна и по модулю, и по направлению; следовательно, движение тела равноускоренное: скорость меняется пропорционально времени, а перемещение — пропорционально квадрату времени. В таком случае график скорости (точнее — ее проекции υ на выбранное направление) представляет собой прямую, проходящую через начало координат (рис. 1, б), а график перемещения (вернее — координаты х) — параболу, вершина которой находится в начале координат (рис. 1, в).
На участке 1-2 сила постоянна, но направлена в противоположную сторону. Скорость линейно падает со временем и в точке 2 обращается в нуль (время действия силы такое же, как на первом участке; значит, такое же и изменение количества движения). График координаты на этом участке — парабола, у которой вершина находится в точке 2. В точке 1 происходит плавный переход одной параболы в другую, так как разрыва скорости в этой точке нет.
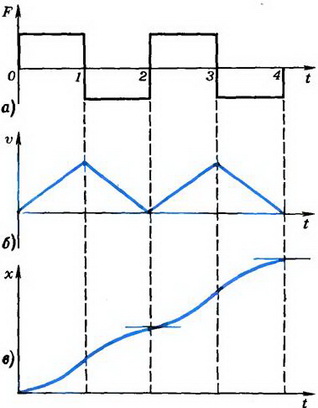
Рис 1.
Дальше рассмотрение ведется аналогично. Как видно из полученных графиков, скорость нигде не меняет знак, лишь периодически обращается в нуль, а координата все время увеличивается. Другими словами, тело все время удаляется от первоначального положения, его движение вовсе не является периодическим, хотя именно такой ответ часто приходится слышать от абитуриентов на вступительных экзаменах.
Задача 2. Два тела массой М1 = 7 кг и М2 =5 кг связаны нитью и лежат на горизонтальном столе (рис. 2, а). К ним через блок, укрепленный на краю стола, подвешивают третье тело массой М = 1 кг. Коэффициент трения между первыми двумя телами и столом μ = 0,l. Определите натяжение обеих нитей и силы трения, действующие на тела. Как изменится ответ, если М = 1,5 кг?
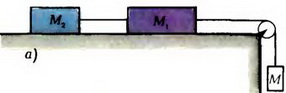

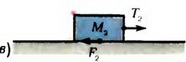
Рис. 2.
Так как значение силы трения существенно зависит от того, движется или покоится тело, прежде всего, выясним, что происходит с данной системой тел. Очевидно, тела будут двигаться, если сила тяжести 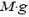 больше максимальной силы трения покоя
больше максимальной силы трения покоя
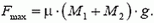
В первом случае 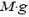 = 10 H, а Fmах = 12 Н; следовательно, движения не возникает. При этом натяжение первой нити, перекинутой через блок, равно
= 10 H, а Fmах = 12 Н; следовательно, движения не возникает. При этом натяжение первой нити, перекинутой через блок, равно
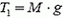 = 10 Н.
= 10 Н.
Рассмотрим силы, действующие на тело массой М1 (рис. 2, б). Так как T1 = 10 Н > 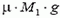 = 7 Н, сила трения достигает своего максимального значения
= 7 Н, сила трения достигает своего максимального значения
 = 7 Н.
= 7 Н.
Эта сила не может уравновесить натяжение T1 первой нити, и вторая нить тоже натягивается. Ее натяжение равно
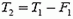 = 3 Н.
= 3 Н.
На тело массой М2 действуют две силы: натяжение нити Т2 и сила трения F2 (рис. 2, в). Так как T2 = 3 Н < 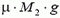 =5 H, сила трения покоя F2 уравновешивает натяжение нити:
=5 H, сила трения покоя F2 уравновешивает натяжение нити:
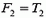 = 3 Н.
= 3 Н.
Во втором случае 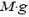 = 15 H; следовательно,
= 15 H; следовательно,  и система тел движется как единое целое. При этом силы трения, действующие на тела, есть силы трения скольжения. Следовательно,
и система тел движется как единое целое. При этом силы трения, действующие на тела, есть силы трения скольжения. Следовательно,
 = 7 Н и
= 7 Н и 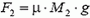 = 5 Н.
= 5 Н.
Обозначим модуль ускорения всех тел через a и запишем второй закон Ньютона для каждого из тел, выбрав соответствующую ось координат:
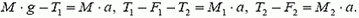
Решая эту систему уравнений, находим
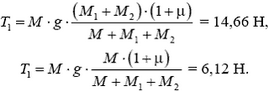
Распространенная ошибка абитуриентов — и в первом случае используется решение, пригодное только для движущейся системы.
Задача 3. По «экватору» внутренней поверхности сферической оболочки массой М с постоянной по модулю скоростью движется небольшой шарик массой m, совершая полный оборот за время Т (рис. 3). Считая, что внешних сил нет и трение отсутствует, определите, с какой силой шарик давит на сферу. Расстояние между центрами тяжести шарика и сферы равно d.
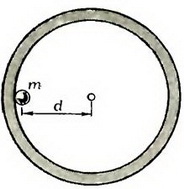
Рис. 3.
Поскольку на систему «сфера — шарик» внешние силы не действуют, центр масс этой системы должен покоиться (что непосредственно следует из законов Ньютона). Это означает, что движутся не только шарик, но и сфера, причем оба они вращаются вокруг оси, проходящей через центр масс системы.
Обозначим расстояние от шарика до центра масс через r, тогда
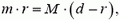 и
и 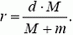
По третьему закону Ньютона сила, с которой шарик давит на сферу, равна по модулю силе, с которой сфера действует на шарик. Она и сообщает шарику центростремительное ускорение
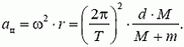
Итак, искомая сила равна по модулю
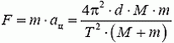
и направлена по радиусу от центра вращения.
Задача 4. Невесомая штанга длиной L одним концом закреплена в идеальном шарнире, а другим опирается на пружину жесткостью k (рис. 4). Определите период малых колебаний штанги в зависимости от положения l на ней груза массой m.
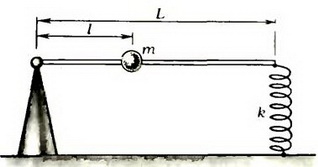
Рис. 4.
Пусть груз сместился по вертикали на расстояние х. При этом пружина деформируется на 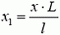 , и со стороны пружины на конец штанги действует сила
, и со стороны пружины на конец штанги действует сила 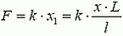 . Штанга невесома, поэтому суммарный момент сил, действующих на нее, должен быть равен нулю (иначе она приобрела бы бесконечно большое угловое ускорение):
. Штанга невесома, поэтому суммарный момент сил, действующих на нее, должен быть равен нулю (иначе она приобрела бы бесконечно большое угловое ускорение):
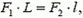
где F2 — сила, действующая на штангу со стороны груза. Следовательно, на груз со стороны штанги действует возвращающая сила, равная
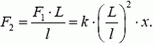
Запишем для груза второй закон Ньютона:
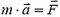 или
или 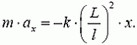
Это — уравнение движения, описывающее свободные гармонические колебания. Оно аналогично уравнению движения груза на пружине, только роль жесткости пружины здесь играет выражение 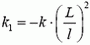 . Таким образом, период колебаний груза, а значит, и невесомой штанги, равен
. Таким образом, период колебаний груза, а значит, и невесомой штанги, равен
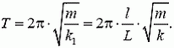
Упражнения
1. Как будет двигаться тело, если действующая на него сила изменяется со временем так, как показано на рисунке 5?
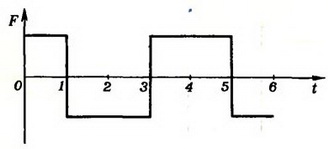
Рис. 5.
2. Три бруска одинаковой массой М = 5 кг лежат на горизонтальном столе. Бруски связаны нитями, которые рвутся при натяжении Т = 20 Н. Коэффициенты трения брусков о стол равны, соответственно, μ1 =0,3, μ2 = 0,2 и μ3 = 0,1. Брусок 3 тянут с силой F, которую постепенно увеличивают. Которая из нитей, скрепляющих бруски, порвется, и при какой минимальной силе F это произойдет? Как изменится ответ, если силу F прикладывать к бруску 1?
3. Груз, подвешенный на нити длиной L, равномерно движется по окружности в горизонтальной плоскости. Найдите период обращения груза, если нить отклонена от вертикали на угол α.
4. Коробка массой М стоит на горизонтальном столе (рис. 6). Коэффициент трения между столом и коробкой μ. Внутри коробки лежит тело массой m, которое может без трения двигаться по дну коробки. Оно прикреплено к стенке коробки пружиной жесткостью k. При какой амплитуде колебаний тела коробка начнет двигаться по столу?
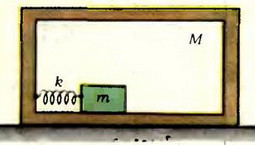
Рис. 6.
Ответы.
1. См. рис. 7.
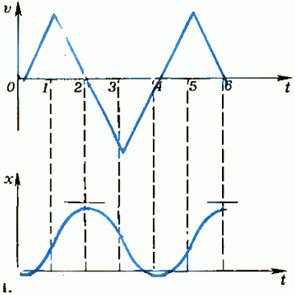
Рис. 7
2. В первом случае раньше всего порвется нить между брусками 2 и 3 (при этом все бруски остаются неподвижными). Это произойдет при силе F1 = 25 Н. Во втором случае порвется нить между брусками 1 и 2 при силе F2 = 37,5 H (бруски движутся).
3. 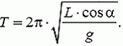
4. 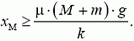
| Выложил | alsak |
| Опубликовано | 09.08.09 |
| Просмотров | 15622 |
| Рубрика | Решение задач |
| Тема | Динамика |