Буздин А.И., Кротов С.С. Повторим гидростатику // Квант
Буздин А.И., Кротов С.С. Повторим гидростатику // Квант. — 1985. — № 2. — С. 48-53.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Школьная программа по физике построена так, что, познакомившись с темой «Гидростатика» в шестом классе, учащиеся больше к ней не возвращаются. По-видимому, принято считать, что эта тема нетрудная. Но, как показывает опыт вступительных экзаменов, задачи и вопросы по гидростатике часто ставят абитуриентов в тупик.
В чем здесь дело? С нашей точки зрения это связано с тем, что в шестом классе школьники еще не готовы к восприятию всех тонкостей физики, они лишь знакомятся с ней. Однако при составлении вопросов и задач для вступительных экзаменов подразумевается, что абитуриент переосмыслил многие темы, в том числе и гидростатику, с более общих позиций, с учетом знания всего курса физики.
В данной статье нам хотелось напомнить основные законы гидростатики и рассмотреть несколько конкретных задач и вопросов, которые в разные годы включались в экзаменационные билеты или задавались абитуриентам в процессе устного экзамена.
Жидкости и газы при движении как целое представляют собой механическую систему, части которой взаимодействуют друг с другом посредством только сил давления. Действительно, когда жидкость (здесь и далее, говоря о жидкости, мы подразумеваем и газ тоже) находится в покое, вязкость не проявляется — жидкое трение возникает лишь при движении слоев жидкости друг относительно друга или относительно твердого тела.
Для жидкости, как известно, выполняется закон Паскаля: давление, производимое на жидкость, передается без изменения в каждую точку жидкости. Если жидкость находится под действием только силы тяжести, давление р увеличивается с глубиной погружения h по закону ![]() , где ρ — плотность жидкости. Поэтому различные участки тела, погруженного в жидкость, испытывают разные силы давления. В результате их суммарного действия возникает выталкивающая сила (архимедова сила). Согласно закону Архимеда, тело, целиком погруженное в жидкость, выталкивается кверху с силой, равной весу вытесненной им жидкости (то есть весу жидкости в объеме этого тела).
, где ρ — плотность жидкости. Поэтому различные участки тела, погруженного в жидкость, испытывают разные силы давления. В результате их суммарного действия возникает выталкивающая сила (архимедова сила). Согласно закону Архимеда, тело, целиком погруженное в жидкость, выталкивается кверху с силой, равной весу вытесненной им жидкости (то есть весу жидкости в объеме этого тела).
Сразу же обратим внимание на тот факт, что закон Архимеда неприменим, когда погруженное тело плотно прижато к стенкам или дну сосуда. Например, известно, что подводная лодка, опустившаяся на илистое дно, под действием силы гидростатического давления прижимается ко дну, а вовсе не выталкивается кверху.
Перейдем теперь к рассмотрению конкретных задач и вопросов.
Вопрос 1. На одной из чашек уравновешенных весов находится стакан с водой и штатив с подвешенным к нему грузом (рис. 1). Что произойдет с равновесием весов, если нить удлинить настолько, чтобы груз оказался в воде?
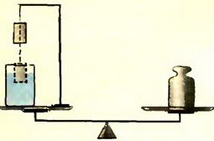
Рис. 1.
Многие абитуриенты считают, что равновесие нарушится. В качестве причины одни называют выталкивающую силу, действующую на груз по закону Архимеда и уменьшающую натяжение нити, а значит, и силу давления штатива на чашку весов. Другие считают, что после погружения в воду груз будет давить на нее с добавочной силой или, что эквивалентно, повысит уровень воды в стакане и тем самым увеличит давление на дно стакана, в результате чего левая чашка перевесит.
Чтобы получить правильный ответ, достаточно понять, что содержимое чашки не меняется в зависимости от положения груза — вне воды или в воде, и поэтому равновесие весов сохраняется. Но что же было неверного в предыдущих рассуждениях?
При опускании груза в воду натяжение нити действительно уменьшится на величину выталкивающей силы, действующей на груз, и поэтому уменьшится сила давления штатива на чашку. Однако, согласно третьему закону Ньютона, на величину выталкивающей силы возрастет сила, действующая со стороны груза на воду и на дно сосуда. Таким образом, давление стакана на чашку увеличится. Причем уменьшение силы давления штатива будет в точности скомпенсировано увеличением силы давления стакана на чашку весов. Ответ, как видим, остается единственным — равновесие не нарушится.
Подумайте, что произошло бы с весами, если бы в чашку с водой опустили палец, не касаясь стенок и дна стакана, или если бы штатив находился на другой чашке уравновешенных весов?
Вопрос 2. В сосуде с водой плавает стакан, в котором находится небольшой шарик (рис. 2). Как изменится уровень воды, если шарик — один раз деревянный, а другой стальной — переложить из стакана в сосуд?
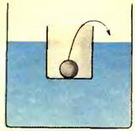
Рис. 2.
Сила давления на дно сосуда равна, очевидно, весу воды, стакана и шарика. Если поставить сосуд (который для простоты можно считать невесомым) на весы, то они покажут вес содержимого, причем их показания не изменятся от того, будет ли шарик находиться в стакане или в сосуде с водой. С другой стороны, весы должны показывать силу, действующую на дно сосуда, которая в начальной ситуации определяется только уровнем воды в сосуде.
В случае, когда из стакана перекладывают деревянный шарик, он будет плавать на поверхности воды, и действующая на дно сосуда сила будет, по-прежнему, определяться лишь уровнем воды. А поскольку эта сила не меняется, уровень воды тоже должен остаться прежним.
Иным будет результат в случае, когда шарик стальной. Такой шарик опустится на дно сосуда, и полная сила давления на дно будет складываться из силы давления воды и силы давления шарика. Полная сила опять-таки не должна измениться, значит, должна уменьшиться сила давления воды. Следовательно, уровень воды в этом случае понизится.
Попробуйте ответить на вопрос: как изменится уровень воды в стакане, где плавает кусок льда с вмороженными в него а) пробкой, б) дробинкой, в) пузырьком воздуха, после того как лед растает?
Вопрос 3. Стальной шарик плавает в ртути. Поверх ртути наливают слой воды, покрывающий шарик (рис. 3). Как изменится глубина погружения шарика в ртуть?
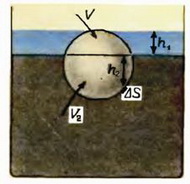
Рис. 3.
Очевидно, возникает желание воспользоваться непосредственно законом Архимеда. Однако трудность состоит в том, что разные части шарика находятся в разных жидкостях, поэтому шарик в целом рассматривать нельзя.
Выберем произвольно малый участок поверхности шарика, находящийся в ртути, и найдем действующую на него силу давления. Ясно, что она будет равна
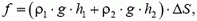
где ρ1 — плотность воды, ρ2 — плотность ртути, ΔS — площадь выбранного участка. Представим эту силу в виде
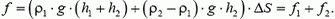
Теперь просуммируем силы давления, действующие на все участки поверхности шарика, соприкасающиеся как со ртутью, так и с водой, и получим две силы: F1 и F2. Сила 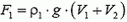 есть выталкивающая сила, действующая на шарик при условии, что он погружен только в воду. Вторая сила
есть выталкивающая сила, действующая на шарик при условии, что он погружен только в воду. Вторая сила 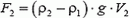 представляет собой силу выталкивания шарика, как если бы он был погружен до уровня ртути в жидкость плотности
представляет собой силу выталкивания шарика, как если бы он был погружен до уровня ртути в жидкость плотности 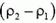 . Таким образом, равнодействующая выталкивающая сила равна
. Таким образом, равнодействующая выталкивающая сила равна
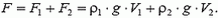
Мы видим, что она складывается из двух частей: вода выталкивает часть шарика, плавающую в ней, а ртуть, сама по себе, выталкивает часть шарика, погруженную в нее. Имеет место как бы принцип независимости сил выталкивания — каждая жидкость вносит в общую силу свой независимый вклад. Хотя интуитивно (и такие ответы действительно встречаются!) могло бы показаться, что ртуть выталкивает шарик, а вода наоборот прижимает его к ртути.
Итак, вода как бы помогает ртути удерживать шарик, он несколько «вылезает» из ртути, и глубина погружения шарика в ртуть уменьшается.
Задача 1. В стакане с водой плавает цилиндрическая деревянная шайба с цилиндрической дыркой. Оси шайбы и дырки параллельны. Площадь дна стакана S, площадь сечения дырки s. Удерживая шайбу на месте, дырку осторожно заполняют маслом, после чего шайбу отпускают. На какую высоту поднимется шайба, если вначале она выступала из воды на величину Н? Плотность масла ρ, плотность воды ρ0.
Прежде всего найдем, на какую высоту поднимется уровень воды в стакане после того как шайбу отпустят. Для этого определим изменение силы давления ΔFд на дно сосуда. С одной стороны,
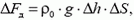
если Δh — изменение уровня воды; с другой стороны, изменение силы давления равно силе тяжести налитого масла:
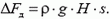
Отсюда получаем
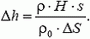
Выталкивающая сила, действующая на шайбу и уравновешивающая ее силу тяжести, определяется давлением воды на ее нижнее основание. Поскольку шайба продолжает плавать, положение ее относительно нового уровня воды в стакане должно остаться неизменным. Следовательно, шайба всплывет как раз на величину Δh.
Подумайте, на сколько поднялась бы шайба, если масло налить вне шайбы, ничего не наливая в дырку?
Задача 2. На камень, выступающий над поверхностью воды на высоту Н, опирается верхним концом тонкая доска длиной l, частично погруженная в воду (рис. 4). При каком минимальном коэффициенте трения между камнем и доской доска будет находиться в равновесии? Плотность воды ρ0, дерева ρ.
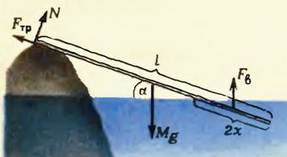
Рис. 4.
На доску действуют четыре силы. Это сила тяжести 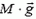 приложенная к центру доски, сила реакции опоры
приложенная к центру доски, сила реакции опоры 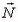 , приложенная к точке касания с камнем и перпендикулярная к доске, сила трения
, приложенная к точке касания с камнем и перпендикулярная к доске, сила трения 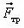 , действующая в той же точке, но направленная по касательной к доске, и выталкивающая сила
, действующая в той же точке, но направленная по касательной к доске, и выталкивающая сила 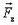 .
.
До сих пор нам было достаточно знать лишь модуль архимедовой силы. Теперь же оказывается необходимым знать, где приложена эта сила. Выделим мысленно в жидкости объем произвольной формы. В равновесии действующая на жидкость в этом объеме сила тяжести уравновешивается силами гидростатического давления, то есть выталкивающей силой. Момент силы тяжести относительно центра масс выделенного участка жидкости равен, очевидно, нулю. Значит, должна быть равна нулю и сумма моментов сил. давления. Заменяя выделенный объем жидкости твердым телом такой же формы, убеждаемся, что действующие на него со стороны окружающей жидкости силы не изменятся. Отсюда можно заключить, что суммарное действие сил давления эквивалентно действию силы, направленной по вертикали и проходящей через центр масс вытесненного объема жидкости. Подчеркнем, что таким образом мы находим лишь линию действия выталкивающей силы, но ничего не можем сказать о конкретной точке ее приложения.
Итак, в данном случае выталкивающая сила направлена вертикально вверх и проходит через середину погруженной части доски (через центр масс вытесненного объема воды).
Пусть площадь сечения доски S, длина погруженной части доски 2х, а угол, который доска составляет с горизонтом (с поверхностью воды), α. Тогда 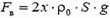 и
и 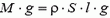 . Поскольку нас интересует минимальное значение коэффициента трения доски о камень, можно считать, что
. Поскольку нас интересует минимальное значение коэффициента трения доски о камень, можно считать, что 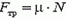 .
.
Так как доска находится в равновесии, сумма всех действующих на доску сил равна нулю. Запишем это условие, спроектировав все силы на направления касательной к доске и нормали к ней:
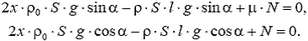
Поделив почленно эти уравнения друг на друга, найдем, что
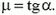
С другой стороны, как это видно из рисунка 4,
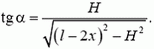
Величину х можно найти из условия равенства нулю суммы моментов всех сил, действующих на доску. Удобнее всего рассмотреть моменты сил относительно точки касания доски и камня (точки О), поскольку при этом моменты сил трения и реакции опоры будут равны нулю.
Линия действия архимедовой силы проходит через центр масс погруженной части доски, значит, ее плечо относительно точки О равно 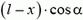 . Плечо силы тяжести равно
. Плечо силы тяжести равно  . Условие равенства нулю суммарного момента сил имеет вид
. Условие равенства нулю суммарного момента сил имеет вид
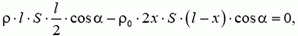
или
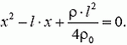
Отсюда находим
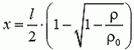
(второй корень следует отбросить, так как он не удовлетворяет условию 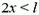 ).
).
Тогда окончательно получаем
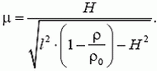
В условии задачи было сказано, что доска тонкая. Как это использовалось при решении?
Отметим, что вопрос о моменте выталкивающей силы исключительно важен при рассмотрении устойчивости плавания тел. В кораблестроении вводится специальное понятие о метацентре — точке пересечения линии действия выталкивающей силы в наклонном положении корабля с плоскостью его симметрии (рис. 5). Метацентр (точка М) не должен опускаться ниже центра тяжести корабля (точка О), иначе вращательный момент архимедовой силы не сможет вернуть корабль в вертикальное положение.
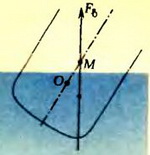
Рис. 5.
Задача 3. В аквариум прямоугольного сечения налита вода (плотность воды ρ = 103 кг/м3) до высоты Н = 0,5 м. Определите силу, действующую на стенку аквариума длиной l = 1 м, и момент сил давления на эту стенку относительно ее нижнего ребра.
В данном случае давление меняется с глубиной погружения h, причем меняется по линейному закону 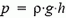 . Не вызывает сомнения, что равнодействующая всех сил давления направлена горизонтально. А чему равен ее модуль? Обычно при ответе на этот вопрос используют формулу
. Не вызывает сомнения, что равнодействующая всех сил давления направлена горизонтально. А чему равен ее модуль? Обычно при ответе на этот вопрос используют формулу 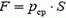 , где
, где 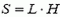 — площадь соприкосновения воды со стенкой, а
— площадь соприкосновения воды со стенкой, а 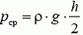 — среднее давление, равное давлению на середине глубины. И такой ответ, безусловно, верный. Однако не каждый абитуриент может объяснить, почему используется именно это давление в качестве среднего. Попробуем это сделать.
— среднее давление, равное давлению на середине глубины. И такой ответ, безусловно, верный. Однако не каждый абитуриент может объяснить, почему используется именно это давление в качестве среднего. Попробуем это сделать.
Рассмотрим прямоугольную призму (из материала плотности ρ) высотой l, в основании которой лежит прямоугольный равнобедренный треугольник со стороной Н. Поставим эту призму на горизонтальную поверхность (рис. 6). Нетрудно видеть, что сила давления призмы на поверхность по модулю совпадает с силой давления воды на боковую поверхность аквариума (вследствие одинаковости распределения давлений по поверхности соприкосновения). Но сила давления призмы — это ее вес, поэтому
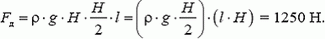
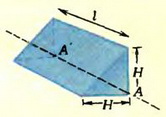
Рис. 6.
Итак, действительно в качестве среднего давления воды следует взять давление на середине глубины.
Второй вопрос задачи — более сложный, поскольку и давление меняется с глубиной, и плечи соответствующих сил давления также зависят от глубины. Ссылаясь на аналогию с предыдущим результатом, иногда предлагают для нахождения момента сил давления использовать среднюю силу давления и «среднее» плечо, равное Н/2. Но это совершенно неправильно. Чтобы получить верный ответ, действительно следует воспользоваться аналогией, но аналогией с призмой, упоминавшейся выше. Для нее искомый момент есть произведение силы тяжести призмы на плечо относительно прямой АА' (см. рис. 6). Линия действия силы тяжести находится на расстоянии Н/3 от ребра АА' (в однородном треугольнике центр масс находится в точке пересечения медиан), поэтому
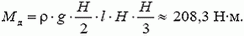
При решении задачи мы нигде не учитывали атмосферное давление. Подумайте, может ли оно изменить ответ? И еще: как изменится сила давления на стенку, если эту стенку сделать резиновой?
Вопрос 4. Что произойдет с глубиной погружения шарика, плавающего в стакане с водой, если стакан начнет с ускорением двигаться вверх?
Рассмотрим систему вода плюс плавающий в ней шарик. Пусть она движется вверх с ускорением а. Это ускорение создается за счет разности сил давления Na со стороны дна стакана и силы тяжести системы 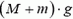 , где М — масса воды, а m — масса шарика:
, где М — масса воды, а m — масса шарика:
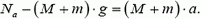
Пока система покоилась, сила давления N0 на дно стакана определялась соотношением
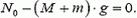
Сравнивая силы Na и N0, видим, что
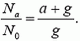
Покажем, что давление в любой точке жидкости увеличилось в такое же число раз. Выделим «водяной» цилиндр сечением ΔS, одно из оснований которого совпадает с поверхностью воды, а другое находится на глубине h. Запишем уравнение движения этого цилиндра в вертикальном направлении:
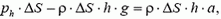
где ph — давление воды на глубине h, ρ — плотность воды. Мы видим, что
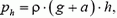
то есть по сравнению со статическим случаем оно возросло в 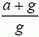 раз. Следовательно, во столько же раз увеличилась выталкивающая сила. Запишем теперь уравнение движения шарика по вертикали:
раз. Следовательно, во столько же раз увеличилась выталкивающая сила. Запишем теперь уравнение движения шарика по вертикали:
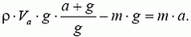
Отсюда получаем, что объем Va погруженной части шарика при ускоренном движении стакана вверх не зависит от ускорения системы и равен
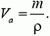
Следовательно, глубина погружения шарика в воду не изменится.
Задача 4. Аквариум, имеющий форму куба с ребром L, до половины наполнен водой и приведен в движение с горизонтальным ускорением 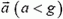 . Считая, что к моменту начала движения системы аквариум — вода как целого вода не расплескалась, определите форму поверхности воды и давление в точке М (рис. 7).
. Считая, что к моменту начала движения системы аквариум — вода как целого вода не расплескалась, определите форму поверхности воды и давление в точке М (рис. 7).
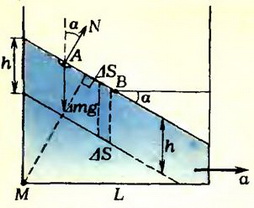
Рис. 7.
Сразу же скажем, что поверхность воды будет представлять собой часть плоскости, наклоненной к горизонту под углом α. Теперь обоснуем это и найдем угол α.
Выделим небольшой объем жидкости массой Δt вблизи произвольной точки А поверхности воды. Равнодействующая сил давления со стороны всей остальной воды будет перпендикулярна поверхности в данном месте. Пусть она равна 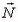 и образует угол α с вертикалью. Тогда выделенный участок поверхности (поскольку он мал, его можно считать плоским) образует тот же угол α с горизонтом (почему?).
и образует угол α с вертикалью. Тогда выделенный участок поверхности (поскольку он мал, его можно считать плоским) образует тот же угол α с горизонтом (почему?).
Запишем уравнения движения нашего объема воды, спроектировав все силы и ускорения на вертикальную и горизонтальную оси:
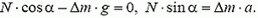
Отсюда получаем
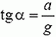
— угол наклона поверхности не зависит от выбора точки А и определяется только отношением a/g.
Выберем теперь в воде плоскость, параллельную поверхности воды и отстоящую от нее по вертикали на расстояние h. Покажем, что во всех ее точках давление воды ph будет определяться по формуле 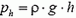 . Действительно, выделим в воде наклонный цилиндр с образующей длины h и основаниями ΔS. По вертикали этот объем не движется, поэтому сумма проекций всех действующих на него сил на вертикальное направление равна нулю:
. Действительно, выделим в воде наклонный цилиндр с образующей длины h и основаниями ΔS. По вертикали этот объем не движется, поэтому сумма проекций всех действующих на него сил на вертикальное направление равна нулю:
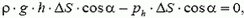
где первое слагаемое — это сила тяжести цилиндра, а второе — вертикальная проекция силы давления на нижнее основание цилиндра. Отсюда получаем
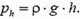
Таким образом, поверхностями постоянного давления будут плоскости, параллельные свободной поверхности воды.
Для нахождения давления в точке М заметим, что из-за несжимаемости воды точка В (середина) остается на месте. Следовательно,
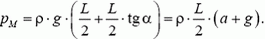
Было ли нами где-нибудь использовано условие 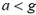 ? Найдите, каковы будут силы давления воды на стенки и дно аквариума при его ускоренном движении?
? Найдите, каковы будут силы давления воды на стенки и дно аквариума при его ускоренном движении?
Расставаясь с читателем, мы надеемся, что при подготовке к вступительным экзаменам он внимательно отнесется к теме «Гидростатика» и не захочет разделить участь «плавающих тел, подверженных действию выталкивающих сил».
Упражнения
1. Ртутный манометр (рис. 8) состоит из двух трубок с площадью сечения S1 и S2, причем S1/S2 = 2. На сколько изменилось измеряемое давление, если уровень ртути в левом колене поднялся на Δh = 10 мм?
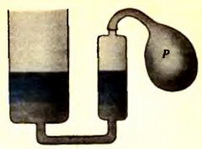
Рис. 8.
2. В бочку с водой упал стеклянный диск. Его диаметр D = 30 см, толщина h = 5 мм, плотность стекла ρ = 2,6·103 кг/м3. Чтобы его достать, в бочку опустили трубку диаметром d = 10 см, плотно прижали ее к диску, выкачали воду и стали медленно поднимать вверх. Определите, до какого расстояния до поверхности воды можно таким способом поднять, диск.
3. Воронка массой М, имеющая форму усеченного конуса с радиусом основания R, стоит на столе. Края воронки плотно прижаты к поверхности стола. Сколько воды будет налито в воронку к моменту ее отрыва от стола, если высота уровня воды в воронке в этот момент равна h?
4. Цилиндрическую гирю, подвешенную к динамометру, опускают в воду, пока уровень воды в сосуде не изменится на Δh = 8 см (рис. 9). Показание динамометра при этом изменилось на ΔF = 0,5 H. Определите сечение сосуда.
5. В сосуде с водой плавает кусок льда, в середину которого вмерзла свинцовая дробинка. Масса льда М, масса дробинки m. Температура воды в сосуде 0 °С. Какое наименьшее количество теплоты надо сообщить системе, чтобы дробинка начала тонуть? Плотность свинца ρ2, льда ρ1, удельная теплота плавления льда λ.
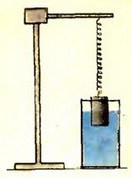
Рис. 9.
6. Плотность раствора соли меняется с глубиной по закону 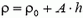 , где ρ0 = 1 г/см3, А = 0,02 г/см4. В раствор опущены два шарика, связанные нитью. Объемы шариков V1 = 0,l см3 и V2 = 0,2 см3, их массы t1 = 0,13 г и t2 = 0,34 г. Глубина погружения первого шарика в состоянии равновесия оказалась равной h1 = 20 см. При этом нить натянута. Определите длину нити.
, где ρ0 = 1 г/см3, А = 0,02 г/см4. В раствор опущены два шарика, связанные нитью. Объемы шариков V1 = 0,l см3 и V2 = 0,2 см3, их массы t1 = 0,13 г и t2 = 0,34 г. Глубина погружения первого шарика в состоянии равновесия оказалась равной h1 = 20 см. При этом нить натянута. Определите длину нити.
7. Где сильнее горит газ — на первом или на последнем этаже четырнадцатиэтажного жилого дома?
8. В стакане, доверху наполненном водой и закрытом сверху, плавает деревянный шарик. Как изменится сила давления шарика на крышку, если сосуд привести в движение с ускорением 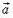 , направленным вертикально вверх?
, направленным вертикально вверх?
Ответы.
1. 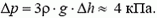
2. 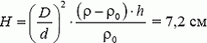 (здесь ρ0 = 103 кг/м3 — плотность воды).
(здесь ρ0 = 103 кг/м3 — плотность воды).
3. 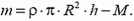
4. 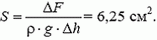
5. 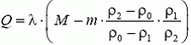 (здесь ρ0 — плотность воды).
(здесь ρ0 — плотность воды).
6. l = 12,5 см.
7. Скорость сгорания газа определяется разностью давления газа и атмосферного давления. Газ, находящийся в трубах (под небольшим давлением), легче воздуха. Поэтому уменьшение давления воздуха при подъеме на четырнадцатый этаж больше, чем уменьшение давления газа. Значит, на верхнем этаже газ должен гореть сильнее.
8. Сила давления на крышку увеличится.
| Выложил | alsak |
| Опубликовано | 16.07.09 |
| Просмотров | 22990 |
| Рубрика | Решение задач |
| Тема | Гидростатика |