Секержицкий В.С. О векторных способах решения избранных задач кинематики
Секержицкий В.С. О векторных способах решения избранных задач кинематики // Фізіка: праблемы выкладання. – Вып. 6. – С. 111-116.
В ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные, на первый взгляд, задачи в подстановочные, решаемые практически устно. В данной статье мы рассмотрим возможность применения векторных способов к решению задач кинематики, большинство из которых предлагались в различные годы на олимпиадах школьников по физике.
1. Некоторые методы теоретической механики предполагают применение достаточно простого математического аппарата, вполне доступного студентам младших курсов вузов и учащимся старших классов (особенно с углубленным изучением физики). К таким методам относится, в частности, использование векторных способов решения задач кинематики. При изучении механики в школе предполагается знакомство с векторным способом кинематического описания движения (вводятся понятия векторов перемещения, скорости и ускорения), но значительно больше внимания уделяется координатному и естественному способам. Вместе с тем в ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные, на первый взгляд, задачи в подстановочные, решаемые практически устно.
В данной статье мы рассмотрим возможность применения векторных способов к решению задач кинематики, большинство из которых предлагались в различные годы на олимпиадах школьников по физике, т е считаются в школьном курсе физики задачами повышенной трудности.
2. При движении тела (материальной точки) его перемещение можно рассматривать как геометрическую сумму нескольких последовательных перемещений, например,
![]() (1)
(1)
Соответствующий уравнению (1) многоугольник перемещений (треугольник в данном случае) представлен на рис. 1. Изменение скорости тела
![]() (2)
(2)
Этому выражению соответствует треугольник скоростей (рис. 2).
При движении тела с постоянным по величине и направлению ускорением ![]() выражение для скорости в любой момент времени t имеет вид:
выражение для скорости в любой момент времени t имеет вид:
![]() (3)
(3)
где ![]() при t = 0.
при t = 0.
В общем случае направления векторов начальной скорости ![]() и ускорения
и ускорения ![]() могут не совпадать. Треугольник скоростей, соответствующий выражению (3), приведен на рис. 3.
могут не совпадать. Треугольник скоростей, соответствующий выражению (3), приведен на рис. 3.
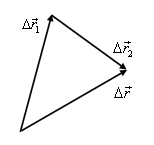
Рис. 1.
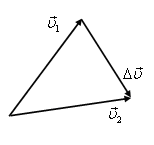
Рис. 2.
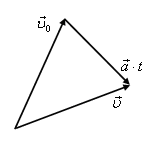
Рис. 3.
Вектор перемещения при этом определяется следующим образом:
![]() (4)
(4)
Треугольники перемещений представлены на рис. 4, а–в.
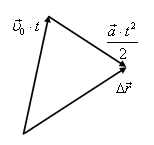
а
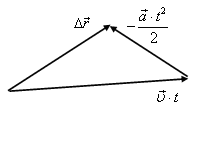
б
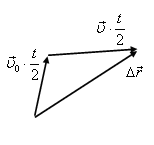
в
Рис. 4.
Наиболее эффективно применение векторного способа, основанного на построении треугольников скоростей и перемещений в тех случаях, когда известны направления векторов ускорения и одной из скоростей (например, начальной). Это относится, в частности, к задачам о движении тела под действием силы тяжести. Рассмотрим примеры.
Задача 1. Тело брошено вверх перпендикулярно плоскости, наклоненной под углом a к горизонту. На каком расстоянии от места броска тело упадет на эту наклонную плоскость? Сопротивлением движения пренебречь.
Решение. На рис. 5 изображен треугольник перемещений, соответствующий условию задачи и соотношению ![]() . Легко видеть, что
. Легко видеть, что ![]() , откуда время движения
, откуда время движения ![]() . Тогда искомое расстояние
. Тогда искомое расстояние ![]() .
.
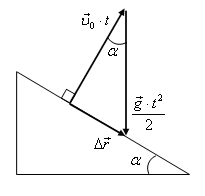
Рис. 5
Задача 2. На наклонную плоскость с углом a свободно падает мяч без начальной скорости. Пролетев расстояние h, он упруго отразился от плоскости. На каком расстоянии от места удара мяч упадет на плоскость вторично? Определите величину и направление его скорости в этот момент. Сопротивлением движению пренебречь.
Решение. При упругом ударе угол падения равен углу отражения, и скорость u0 отскока мяча равна конечной скорости его падения с высоты h: ![]() . Треугольник перемещений BCD (рис. 6), соответствующий соотношению
. Треугольник перемещений BCD (рис. 6), соответствующий соотношению ![]() , равнобедренный. Тогда
, равнобедренный. Тогда ![]() и искомое расстояние
и искомое расстояние
![]()
Соотношению ![]() соответствует треугольник перемещений BED (рис. 6), из которого по теореме синусов находим:
соответствует треугольник перемещений BED (рис. 6), из которого по теореме синусов находим:
![]()
Величину скорости u можно определить по теореме косинусов из треугольника ECD:
![]()
Тогда
![]()
Итак, мяч вторично падает на наклонную плоскость со скоростью ![]() , вектор которой направлен к плоскости под углом
, вектор которой направлен к плоскости под углом ![]() .
.
Заметим, что основанные на принципе независимости движений координатные способы решения данных задач более трудоемкие, чем предложенные выше. Другие примеры решения задач кинематики с использованием треугольников перемещений и скоростей приведены в [1].
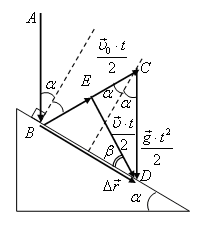
Рис. 6.
При движении двух материальных точек относительно некоторой систему отсчета, зная их перемещения ![]() , можно вычислить перемещение второго тела относительно первого:
, можно вычислить перемещение второго тела относительно первого:
![]() (5)
(5)
Разность скоростей тел (относительная скорость) определяется выражением:
![]() (6)
(6)
соответствующим закону сложения скоростей Галилея:
![]() (7)
(7)
где ![]() – скорости первого и второго тел в неподвижной системе отсчета (естественно, «неподвижность» системы относительна),
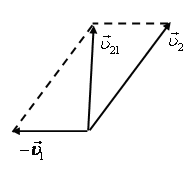
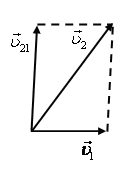
– скорости первого и второго тел в неподвижной системе отсчета (естественно, «неподвижность» системы относительна), ![]() – скорость второго тела относительно первого. Треугольник и параллелограммы скоростей, соответствующие формулам (6) и (7), представлены на рис. 7, а-в.
– скорость второго тела относительно первого. Треугольник и параллелограммы скоростей, соответствующие формулам (6) и (7), представлены на рис. 7, а-в.
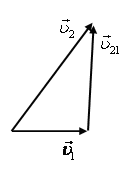
а
б
в
Рис. 7.
Применим формулы (6) и (7) к решению задач
Задача 3. Две частицы брошены одновременно из одной точки с одинаковыми по модулю скоростями u: первая – вертикально вверх, вторая – горизонтально. Найдите расстояние между ними спустя время t. Сопротивлением движению пренебречь.
Решение. Ускорения частиц одинаковы и равны g (движение под действием силы тяжести). Следовательно, относительное движение равномерное и прямолинейное, т.е. вторая частица движется относительно первой с постоянной скоростью ![]() (рис. 8). Тогда искомое расстояние
(рис. 8). Тогда искомое расстояние ![]() .
.
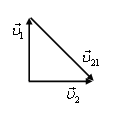
Рис. 8.
Задача 4. Две частицы находятся на одной высоте на расстоянии l друг от друга. Им одновременно сообщили одинаковые по величине скорости, направления которых показаны на рис. 9. Найдите минимальное расстояние между частицами в процессе их движения. Частицы движутся в одной вертикальной плоскости, сопротивление отсутствует.
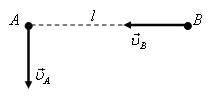
Рис. 9.
Решение. Свяжем систему отсчета с телом А. Тогда (рис 10)
![]()
Ускорения обеих частиц одинаковы и равны g в системе отсчета, связанной с землей. Следовательно, относительная скорость ![]() постоянна по величине и направлению, траектория относительного движения – прямая. Искомое наименьшее расстояние между частицами (между точкой А и траекторией относительного движения на рис. 10)
постоянна по величине и направлению, траектория относительного движения – прямая. Искомое наименьшее расстояние между частицами (между точкой А и траекторией относительного движения на рис. 10) ![]() .
.
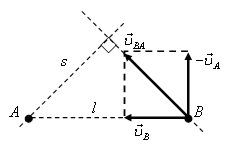
Рис. 10.
Задача 5. Собственная скорость пловца в п раз (n > 1) меньше скорости течения. Под каким углом к течению он должен стараться плыть, чтобы при переправе через реку снос был минимальным?
Решение. Воспользуемся формулой (7) и треугольником скоростей, представленным на рис 7, а. Здесь ![]() – скорость течения,
– скорость течения, ![]() – собственная скорость пловца (относительно воды),
– собственная скорость пловца (относительно воды), ![]() – скорость пловца относительно неподвижной системы отсчета (берега). Так как u1 > u21, го снос будет иметь место при любом направлении вектора
– скорость пловца относительно неподвижной системы отсчета (берега). Так как u1 > u21, го снос будет иметь место при любом направлении вектора ![]() (при движении пловца по течению или против течения снос максимальный). Геометрическое место концов вектора
(при движении пловца по течению или против течения снос максимальный). Геометрическое место концов вектора ![]() для всевозможных его направлений представляет собой полуокружность (рис. 11). Легко видеть, что снос будет минимальным, если вектор
для всевозможных его направлений представляет собой полуокружность (рис. 11). Легко видеть, что снос будет минимальным, если вектор ![]() направлен по касательной к этой полуокружности, т.е.
направлен по касательной к этой полуокружности, т.е. ![]() . Тогда
. Тогда ![]() . Искомый угол
. Искомый угол ![]() .
.
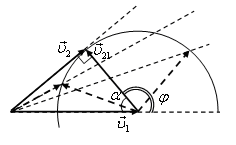
Рис. 11.
Задача 6. Жесткий стержень АВ движется в плоскости рисунка 12, на котором показаны направления скоростей точек А и В. Найдите величину скорости uB, если uA = 5,0 м/с.
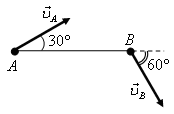
Рис. 12.
Решение. Так как расстояние между точками A и В неизменно (стержень жесткий), то скорость ![]() точки В относительно точки А может быть направлена только перпендикулярно стержню. Учитывая, что
точки В относительно точки А может быть направлена только перпендикулярно стержню. Учитывая, что ![]() , строим параллелограмм скоростей (рис. 13), который в данное случае является прямоугольником. Тогда
, строим параллелограмм скоростей (рис. 13), который в данное случае является прямоугольником. Тогда
![]()
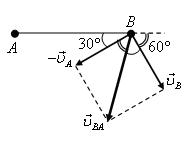
Рис. 13.
Примеры решения аналогичных задач приведены в [2]. Очевидно, что применение векторных способов для решения ряда задач кинематики весьма эффективно, но в IX классе общеобразовательной школы для этого нет достаточной математической (тригонометрической) базы. В классах же с углубленным изучением физики, в курсах по выбору, при подготовке к олимпиадам изучение векторных способов решения задач вполне целесообразно. Опыт преподавания автором на протяжении нескольких лет факультативного спецкурса "Избранные задачи по физике и методы их решения" в лицее №1 г. Бреста показывает, что учащиеся XI класса достаточно легко воспринимают и усваивают векторные способы решения задач.
1. Койфман Ю.Г., Секержицкий В.С. Кинематика: о векторном cnocoбе решения избранных задач // Фокус. – 1993. – №4. – С. 61-68.
2. Секержицкий В.С. Кинематика: относительность движения // Фокус. – 1995. – №2. – С. 77-80.
| Выложил | alsak |
| Опубликовано | 27.12.07 |
| Просмотров | 24943 |
| Рубрика | Решение задач |
| Тема | Кинематика |