Данилин В. Кинематика. Относительность движения //Квант
Данилин В. Кинематика. Относительность движения //Квант. — 1982. — № 10. — С. 48-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Раздел механики, в котором движения описываются без исследования причин, их вызывающих, называется кинематикой. Основная задача кинематики заключается в том, чтобы, зная три кинематические величины: перемещение, скорость и ускорение, найти положение тела в любой момент времени.
Всякое движение относительно, поэтому для его описания можно использовать различные системы отсчета. Все они кинематически равноправны, то есть принципиально позволяют решить ту или иную задачу. Трудно дать какие-либо общие рекомендации по выбору системы отсчета, поскольку он определяется, в основном, конкретными условиями данной задачи. В большинстве случаев следует выбирать ту систему, которая наиболее естественна и в которой решение задачи имеет наиболее простой вид. Например, при рассмотрении движения искусственного спутника Земли с точки зрения земного наблюдателя систему отсчета естественно связать с Землей. При анализе движений различных тел внутри спутника с точки зрения космонавта систему отсчета разумно связать с самим спутником, а с точки зрения земного наблюдателя — опять-таки с Землей.
Иногда приходится переходить от одной системы отсчета к другой. В разных системах описания движения могут выглядеть по-разному: могут различаться траектории движения, перемещения, скорости и ускорения тела. Однако при заданных связях между различными системами отсчета описания одного и того же движения всегда можно связать друг с другом.
А теперь поясним сказанное на конкретных задачах. Большинство из них предлагалось на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Два снаряда выпущены горизонтально вперед один вслед за другим с интервалом времени t со скоростью u из орудия, находящегося на самолете, который летит горизонтально со скоростью υ. Пренебрегая сопротивлением воздуха, найдите: 1) уравнение траектории первого снаряда относительно земли; 2) уравнение траектории первого снаряда относительно самолета; 3) как изменяется положение первого снаряда относительно второго (после обоих выстрелов).
В данном случае выбор системы отсчета фактически определен условием задачи.
Направим оси координат следующим образом: ось X — горизонтально, параллельно курсу самолета, ось Y — вертикально вниз. Начало же системы координат каждый раз будем указывать отдельно.
1) Поместим начало координат в точку, в которой находился самолет в момент вылета первого снаряда (разумеется, и самолет, и снаряд считаются материальными точками). Относительно этой неподвижной системы отсчета начальная (горизонтальная) скорость снаряда равна сумме скоростей снаряда относительно самолета и самого самолета, то есть 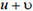 .
.
Тогда горизонтальная и вертикальная координаты снаряда в любой момент времени t таковы:
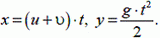
Выражая t из первого равенства и подставляя во второе, получим уравнение траектории снаряда относительно земли:
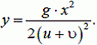
Это безусловно знакомое всем уравнение параболы. Заметим, что уравнение траектории второго снаряда относительно земли будет точно таким же.
2) В этом случае начало системы отсчета надо связать с самолетом. Относительно него начальная скорость снаряда равна u, поэтому горизонтальная координата снаряда будет изменяться по закону 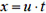 . Вертикальная же координата по-прежнему будет иметь вид
. Вертикальная же координата по-прежнему будет иметь вид 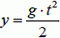 . Сделав аналогичные первому случаю преобразования, получим уравнение траектории снаряда относительно движущегося самолета:
. Сделав аналогичные первому случаю преобразования, получим уравнение траектории снаряда относительно движущегося самолета:
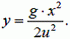
Очевидно, что и здесь траектория движения снаряда — парабола.
3) Для того чтобы описать движение первого снаряда относительно второго, воспользуемся той же системой отсчета, что и для первого случая, то есть поместим начало координат в ту точку, где находился самолет в момент первого выстрела.
Запишем уравнения для координат хi и уi первого снаряда и для соответствующих проекций υ1x и υ1y его скорости:
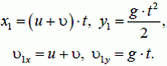
Здесь время t отсчитывается от момента первого выстрела, но по смыслу задачи оно не меньше интервала τ между выстрелами, то есть 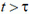 . Аналогичные уравнения для второго снаряда будут иметь вид
. Аналогичные уравнения для второго снаряда будут иметь вид
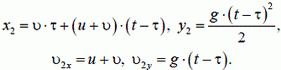
Если наблюдатель связан со вторым снарядом, то относительно него координаты (или проекции скорости) первого снаряда равны разности соответствующих координат (или соответствующих проекций скоростей) первого и второго снарядов в неподвижной системе отсчета:
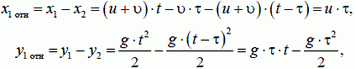
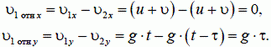
Итак, после обоих выстрелов снаряды по горизонтали движутся с одинаковыми скоростями, так что расстояние между ними не изменяется и остается равным 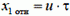 . По вертикали же первый снаряд движется относительно второго с постоянной скоростью
. По вертикали же первый снаряд движется относительно второго с постоянной скоростью 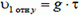 , поэтому расстояние между снарядами с течением времени изменяется по закону
, поэтому расстояние между снарядами с течением времени изменяется по закону 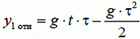 .
.
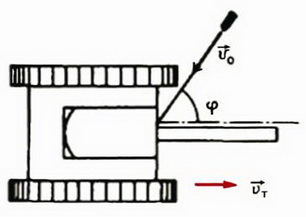
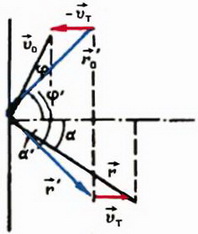
Задача 2. В лобовой щит танка, движущегося со скоростью υт = 54 км/ч, ударяется пуля, летящая со скоростью υ0 = 1800 км/ч под углом φ = 60° к направлению движения танка, и упруго отскакивает от него (рис. 1, а). С какой скоростью 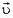 полетит отскочившая пуля?
полетит отскочившая пуля?
а
б
Рис. 1.
Задачу удобно сначала решить в системе отсчета, связанной с танком, а затем перейти в неподвижную систему отсчета.
Относительно танка скорость пули до удара равна 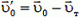 (рис. 1, б). После упругого удара модуль скорости пули
(рис. 1, б). После упругого удара модуль скорости пули 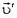 остается прежним
остается прежним 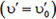 , а угол «отражения» β´ будет равен углу «падения» φ´.
, а угол «отражения» β´ будет равен углу «падения» φ´.
В неподвижной системе отсчета пуля после удара будет двигаться со скоростью
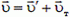 .
.
Модуль и направление этой скорости найдем из рисунка 1, б:
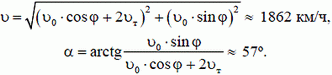
Задача 3. Горизонтальный диск вращается вокруг своей оси, делая п = 5 об/мин. Человек идет вдоль радиуса диска с постоянной скоростью и = 1,5 м/с относительно диска. Как меняется модуль скорости человека относительно земли в зависимости от расстояния r от оси диска? Чему равен модуль этой скорости на расстоянии R = 3 м от оси диска?
а
б
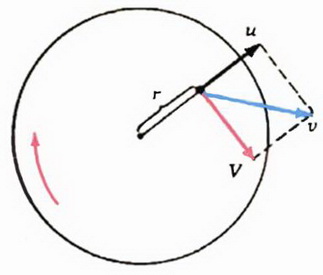
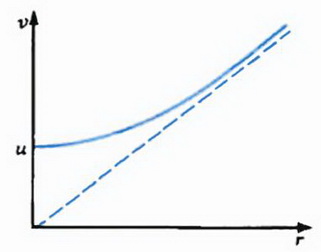
Рис. 2.
В любой точке диска скорость 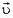 человека относительно земли равна векторной сумме двух скоростей (рис. 2, а): скорости
человека относительно земли равна векторной сумме двух скоростей (рис. 2, а): скорости 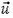 движения человека по диску, направленной вдоль его радиуса, и линейной скорости
движения человека по диску, направленной вдоль его радиуса, и линейной скорости 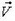 точки диска, в которой находится человек, направленной перпендикулярно радиусу, то есть
точки диска, в которой находится человек, направленной перпендикулярно радиусу, то есть
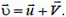
Поскольку модуль V линейной скорости связан с угловой скоростью ω, а значит, и с частотой п вращения диска: 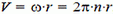 , то модуль скорости человека относительно земли равен
, то модуль скорости человека относительно земли равен
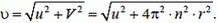
Графически зависимость υ от r представлена на рисунке 2, б.
На расстоянии R от оси диска модуль искомой скорости равен

Задача 4. Колесо радиуса R движется по земле поступательно со скоростью υ0 и вращается с угловой скоростью ω (рис. 3). Найдите тангенциальную и нормальную проекции ускорения некоторой точки А на ободе колеса в неподвижной системе отсчета, связанной с землей.
Напомним, что тангенциальная (касательная) проекция ат ускорения 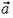 — это проекция на направление касательной к траектории, то есть на направление скорости; ат отвечает за изменение модуля скорости. Нормальная проекция ан — это проекция ускорения
— это проекция на направление касательной к траектории, то есть на направление скорости; ат отвечает за изменение модуля скорости. Нормальная проекция ан — это проекция ускорения 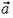 на направление, перпендикулярное (нормальное) к касательной, то есть перпендикулярное к скорости; ан отвечает за изменение направления скорости.
на направление, перпендикулярное (нормальное) к касательной, то есть перпендикулярное к скорости; ан отвечает за изменение направления скорости.
Сначала рассмотрим движение точки А в системе отсчета, связанной с колесом. Здесь эта точка равномерно вращается по окружности радиуса R, так что скорость изменяется только по направлению. Ускорение точки направлено по радиусу к центру колеса и равно по модулю 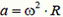 (это ускорение называют также центростремительным).
(это ускорение называют также центростремительным).
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
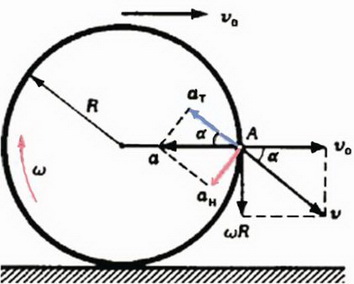
Рис. 3.
Рассмотрим точку А в некоторый момент времени (см. рис. 3). Ее скорость 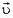 равна по модулю
равна по модулю  и направлена по касательной к траектории, а полное ускорение
и направлена по касательной к траектории, а полное ускорение 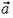 равно по модулю
равно по модулю 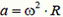 и направлено по радиусу к центру колеса. Найдем тангенциальную и нормальную проекции этого ускорения:
и направлено по радиусу к центру колеса. Найдем тангенциальную и нормальную проекции этого ускорения:
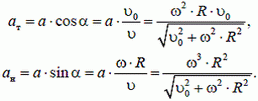
Задача 5*. Тяжелый диск радиуса R скатывается на двух нерастяжимых нитях, намотанных на него (рис. 4). Концы нитей закреплены. Нити при движении диска постоянно натянуты. В некоторый момент угловая скорость диска равна ω, а угол между нитями α. Какова в этот момент скорость центра диска?
Рис. 4
Выберем две системы отсчета: неподвижную, связанную, например, с землей, и подвижную, связанную с центром диска. Таким образом, задача сводится к тому, чтобы найти скорость подвижной системы отсчета относительно неподвижной.
Пусть в данный момент нити касаются диска в точках А и В. В подвижной системе отсчета (связанной с центром диска) скорости 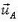 и
и 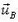 этих точек равны по модулю
этих точек равны по модулю 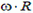 и направлены вдоль нитей. В системе, связанной с землей, скорости
и направлены вдоль нитей. В системе, связанной с землей, скорости 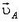 и
и 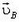 могут быть направлены только перпендикулярно нитям, так как нити всё время натянуты.
могут быть направлены только перпендикулярно нитям, так как нити всё время натянуты.
Обозначим скорость центра диска (скорость подвижной системы отсчета), направленную вертикально вниз, через 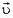 . Тогда
. Тогда
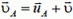 и
и 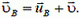
Как видно из рисунка, при сложении соответствующих векторов получаются равные прямоугольные треугольники, из которых
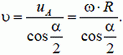
Упражнения
1. Изогнутая трубка длины L = 1 м вращается вокруг вертикальной оси ОО' с угловой скоростью ω = 0,1 рад/с (рис. 5). Открытый конец трубки направлен вертикально вниз, и из него вытекает вода практически без начальной скорости относительно трубки. На расстоянии Н = 10 м ниже отверстия расположена горизонтальная плоскость. Найдите радиус окружности, которую опишет след струи воды на этой плоскости.
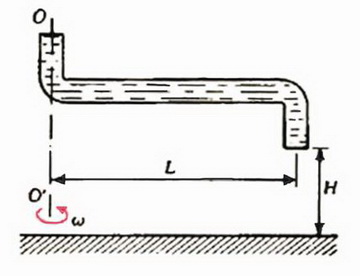
Рис. 5.
2. Гладкий диск радиуса R, плоскость которого горизонтальна, вращается вокруг своей оси. От поверхности диска отрывается небольшое тело, которое без трения скользит по диску. На каком расстоянии от оси оторвалось тело, если за время, пока оно соскользнуло с диска, диск сделал полный оборот?
3. Искусственный спутник Земли запущен с экватора и вращается по круговой орбите в плоскости экватора в направлении вращения Земли. Найдите отношение радиуса орбиты спутника к радиусу Земли, при котором спутник периодически проходит над точкой запуска ровно через двое суток.
4. Как показали радиолокационные измерения, Венера вращается вокруг своей оси в направлении, противоположном ее орбитальному движению. Период осевого вращения Венеры (относительно звезд) Т1 = 243 земных суток. Определите продолжительность солнечных суток на Венере, то есть время Т между двумя последовательными прохождениями Солнца через один и тот же меридиан на этой планете (время от полудня до полудня). Венера обращается вокруг Солнца с периодом Т2 = 225 земных суток.
5. Тяжелый шар радиуса R лежит на горизонтальной плоскости, а в верхней точке шара покоится малое тело. По шару наносят удар, и он начинает двигаться со скоростью υ. На какую высоту подпрыгнет тело после упругого отскока от плоскости? Трением и сопротивлением воздуха пренебречь.
Ответы.
1. 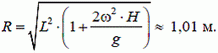
2. 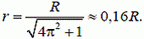
3. 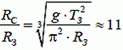 или
или 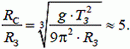
4. 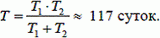
5. 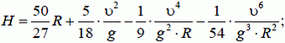 при
при 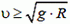 тело свободно падает вниз и подпрыгивает на высоту 2R.
тело свободно падает вниз и подпрыгивает на высоту 2R.
| Выложил | alsak |
| Опубликовано | 13.06.09 |
| Просмотров | 21219 |
| Рубрика | Решение задач |
| Тема | Кинематика |