Коржов Н.И. Задача о веревке на столе
Коржов Н.И. Задача о веревке на столе // Фiзiка: праблемы выкладання. – 2003. – № 5. – С. 65-71.
Пусть однородная веревка длиной L и массой m соскальзывает с горизонтального стола перпендикулярно его краю (рис. 1), и в некоторый момент длина свисающего конца равна х.
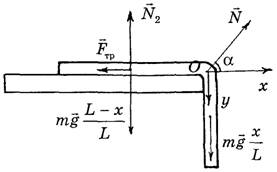
Pис. 1
В общем случае на веревку действуют:
1) сила тяжести 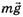 , которую заменим суммой двух сил — силы тяжести
, которую заменим суммой двух сил — силы тяжести
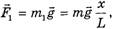 (1)
(1)
действующей на свисающую часть веревки длиной х,и силы тяжести
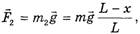 (2)
(2)
действующей на часть веревки, находящейся на столе;
2) сила реакции края стола 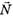 (угол между нею и горизонталью обозначим через α);
(угол между нею и горизонталью обозначим через α);
3) сила нормальной реакции поверхности стола
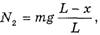
которая компенсируется силой тяжести 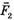 ;
;
4) сила кремния веревки о стол
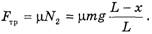 (3)
(3)
Если конец веревки смещается на расстояние Δx за время Δt, то по определению его скорость
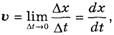 (4)
(4)
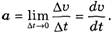 (5)
(5)
Поскольку веревка не является ни материальной точкой, ни абсолютно твердым телом, движущимся поступательно, то второй закон Ньютона в форме 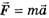 неприменим. Будем применять закон изменения импульса
неприменим. Будем применять закон изменения импульса
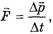
где 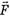 — сумма внешних сил, действующих на систему, а
— сумма внешних сил, действующих на систему, а 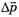 — изменение импульса системы.
— изменение импульса системы.
Если за время Δt скорость куска веревки изменилась с 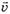 до
до 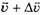 , а масса — с ml до ml + Δml, то импульс этого куска изменился на
, а масса — с ml до ml + Δml, то импульс этого куска изменился на
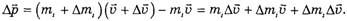
Пренебрегая слагаемым 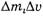 и учитывая, что
и учитывая, что
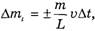
получим с учетом (5)
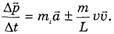 (6)
(6)
Если масса куска веревки увеличивается (т1),то в выражении (6) второе слагаемое имеет знак «+», если уменьшается (т2)— знак «–».
Запишем закон изменения импульса для всей веревки в целом:
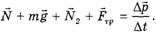
Проецируя на горизонтальную ось с учетом (6), имеем
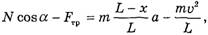
откуда с учетом(3)
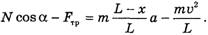 (7)
(7)
Аналогично, проецируя на вертикальную ось, имеем
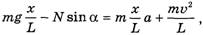
откуда
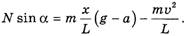 (8)
(8)
Пусть в начальный момент веревка покоится, а со стола свешивается часть веревки длиной l. Нулевой уровень потенциальной энергии выберем на уровне поверхности стола. Тогда в начальном состоянии веревка обладает только потенциальной энергией
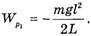 (9)
(9)
В тот момент, когда со стола свешивается часть веревки длиной х > l (конечное состояние), потенциальная энергия веревки
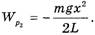 (10)
(10)
Для нахождения работы силы трения найдем силы трения в начальном и конечном состояниях:
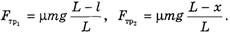
Поскольку сила трения линейно зависит от x,воспользуемся средним значением силы трения
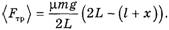 (11)
(11)
Тогда работа силы трения
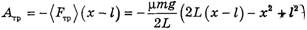 (12)
(12)
В соответствии с законом сохранения энергии (при условии равенства скоростей всех элементов веревки)
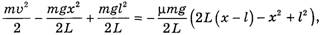
откуда
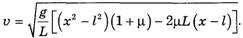 (13)
(13)
В соответствии с выражением (5) с учетом равенства (4)
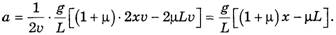 (14)
(14)
С учетом формул (13) и (14) после преобразований формулы (7) и (8) примут вид
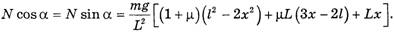 (15)
(15)
Значит, α = 45° и
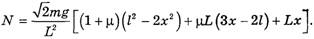 (16)
(16)
Очевидно, что по формуле (15) можно также вычислять силу Tнатяжения веревки в сечении, находящемся на краю стола. Это следует из третьего закона Ньютона.
А сейчас перейдем к анализу выражения (16) при различных начальных условиях.
1. Трение отсутствует (μ = 0), вся веревка вначале лежит на столе (l = 0).В этом случае
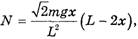 (17)
(17)
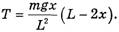 (18)
(18)
Сравните эти выражения с соответствующими формулами в [1] (№ 185), [2] (№ 8.21), [3]. Причина расхождения очевидна — в указанных источниках второй закон Ньютона применен вне границ его применимости. Из формул (17) и (18) следует, что при длине свисающего конца веревки 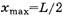 край стола перестанет действовать на веревку, и натяжение веревки у края стола исчезает. Это говорит о том, что после данного момента горизонтальная составляющая импульса веревки (а она к этому моменту равна
край стола перестанет действовать на веревку, и натяжение веревки у края стола исчезает. Это говорит о том, что после данного момента горизонтальная составляющая импульса веревки (а она к этому моменту равна 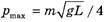 ) не должна изменяться (в горизонтальном направлении внешняя сила перестает действовать на веревку). Значит, продолжающий движение по столу конец веревки должен уже не сразу изменять направление своего движения на вертикальное, а «вылетать» за край стола в сторону, что подтверждает и опыт с металлической цепочкой, движущейся по горизонтальной стеклянной поверхности стола. Внутренние же силы (силы упругости) могут изменять только скорости отдельных частей веревки. Итак, начиная с момента, когда
) не должна изменяться (в горизонтальном направлении внешняя сила перестает действовать на веревку). Значит, продолжающий движение по столу конец веревки должен уже не сразу изменять направление своего движения на вертикальное, а «вылетать» за край стола в сторону, что подтверждает и опыт с металлической цепочкой, движущейся по горизонтальной стеклянной поверхности стола. Внутренние же силы (силы упругости) могут изменять только скорости отдельных частей веревки. Итак, начиная с момента, когда 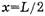 , прямолинейность концов веревки нарушается, и различные участки веревки уже не имеют равных скоростей. Тогда нет смысла искать скорость веревки в момент ее полного сползания со стола ([4]-[6]). В [1] и [3] сделаны попытки объяснить, почему задача разрешима только при
, прямолинейность концов веревки нарушается, и различные участки веревки уже не имеют равных скоростей. Тогда нет смысла искать скорость веревки в момент ее полного сползания со стола ([4]-[6]). В [1] и [3] сделаны попытки объяснить, почему задача разрешима только при 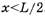 , однако, как показано выше, выражения для N иTполучены неверные. Наконец, запишем выражения для скорости и ускорения веревки при указанных выше условиях:
, однако, как показано выше, выражения для N иTполучены неверные. Наконец, запишем выражения для скорости и ускорения веревки при указанных выше условиях:
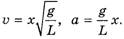 (20)
(20)
2. Трение отсутствует (μ = 0), но в начальный момент веревка удерживается на столе так, что с края стола свешивается ее часть длиной l. В этом случае из соотношений (15) и (16) имеем:
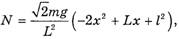 (21)
(21)
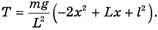 (22)
(22)
Очевидно, что при
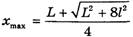
(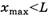 , так как
, так как 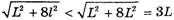 ) веревка, как и в первом случае, перестанет действовать на край стола. Значит, искать ее скорость в момент полного соскальзывания со стола ([7]) бессмысленно по указанной выше причине.
) веревка, как и в первом случае, перестанет действовать на край стола. Значит, искать ее скорость в момент полного соскальзывания со стола ([7]) бессмысленно по указанной выше причине.
3. Трение между столом и веревкой есть, причем в начальный момент с края стола свешивается конец веревки длиной l. Пусть при данных условиях веревка находится на грани скольжения. В этом случае из условия равновесия веревки
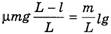
найдем коэффициент трения
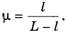 (23)
(23)
Тогда из выражений (15) и (16) с учетом равенства (23) имеем:
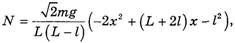 (24)
(24)
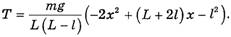 (25)
(25)
При
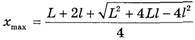
силы N и T вновь исчезают. Необходимо установить, выполняется ли условие 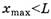 . С помощью производной легко установить, что выражение
. С помощью производной легко установить, что выражение
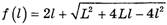
принимает максимальное значение 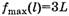 при
при 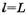 , откуда сразу следует, что
, откуда сразу следует, что 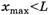 . Итак, даже при наличии трения при указанных выше условиях веревка вновь начинает вылетать за край стола ранее, чем вся она с него сползет (ср. с [8], № 1.67 (в)).
. Итак, даже при наличии трения при указанных выше условиях веревка вновь начинает вылетать за край стола ранее, чем вся она с него сползет (ср. с [8], № 1.67 (в)).
1. Буховцев Б.Б., Кривченков В.Д., Мякишев Г.Я., Сараево И.М. Сборник задач по элементарной физике. — М.: Наука, 1987.
2. Гельфгат И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с ответами, указаниями, решениями. — М.: Илекса, 2001.
3. Гельфгат И. Сколько веревочке ни виться // Квант. — 1993. — № 1/2.
4. Гольдфарб Н.И. Сборник вопросов и задач по физике. — М.: Высшая школа, 1973.
5. Парфентъева Н.А., Фомина М.Ф. Физика. Теория, задачи, решения. — Мн.: Альфа, 1995.
6. Жилко В.В. Физика на вступительных экзаменах в вузы. Конкурсные задачи и решения. — Мн.: Красико-Принт, 2002.
7. Лернер Г.И. Физика. Решение школьных и конкурсных задач. Уроки репетитора. — М.: Новая школа, 1996.
8. Савельев И.В. Сборник вопросов и задач по общей физике. — М.: Наука, 1988.
| Выложил | alsak |
| Опубликовано | 01.06.09 |
| Просмотров | 26273 |
| Рубрика | Решение задач |
| Тема | Законы сохранения Динамика |