Слободянюк А.И. Анализ применимости некоторых физических моделей
Слободянюк А.И. Анализ применимости некоторых физических моделей // Фiзiка: праблемы выкладання.. – 1996. – Вып. 2. – C. 16-26.
В школьном курсе физики также широко используется целый ряд общеупотребительных моделей физических систем и физических явлений. Однако условия применимости этих моделей либо вообще не оговариваются, либо ограничиваются общими и неконкретными рассуждениями. Исходя из сказанного, необходимо четко сформулировать критерии применимости модели и проанализировать используемые модели с точки зрения этих критериев.
Любое описание физических явлений, любая физическая теория оперирует только с моделями физических систем и явлений. Построение модели (прежде всего речь идет о математической модели) предполагает явное выделение некоторых существенных свойств моделируемого объекта и пренебрежение теми свойствами, которые являются второстепенными, несущественными.
В школьном курсе физики также широко используется целый ряд общеупотребительных моделей физических систем (материальная точка, абсолютно твердое тело, идеальный газ и т.д.) и физических явлений (например, изотермический и адиабатный процессы, квазистационарный ток и т.д.). Однако условия применимости этих моделей либо вообще не оговариваются, либо ограничиваются общими и неконкретными рассуждениями. На мой взгляд, вопрос о рамках применимости той или иной модели имеет принципиальное значение потому, что, во-первых, является фундаментом построения любой теории и, во-вторых, служит глубокому неформальному пониманию физической сущности теории, следовательно, пониманию самой физики.
Исходя из сказанного, необходимо четко сформулировать критерии применимости модели и проанализировать используемые модели с точки зрения этих критериев. Как уже было отмечено, любая модель, даже самая совершенная, есть упрощенное описание, в котором могут исчезнуть некоторые качественно иные аспекты явления. Поэтому первый критерий правомочности использования модели является качественным.
Критерий 1. Цель теоретического описания. Существуют ли в рамках используемой модели те явления, которые требуется описать.
Любая модель есть приближенное описание реальности, поэтому второй критерий ее применимости количественный.
Критерий 2. Точность теоретического описания. Можно ли в рамках используемой модели пренебречь погрешностями моделирования, т.е. погрешностями, возникающими вследствие пренебрежения некоторыми деталями, факторами, которые считаются несущественными при построении модели.
Проанализируем с позиций сформулированных критериев некоторые широко используемые в школьном курсе физики модели. Сначала рассмотрим некоторые модели физических систем, а затем модели физических явлений.
1. Материальная точка – модель реального тела, размерами которого в данных условиях можно пренебречь. Сразу отметим главное и основное отличие материальной точки от реального тела – отсутствие геометрических размеров. Материальную точку можно «наделить» множеством физических характеристик: массой, зарядом, импульсом, энергией, моментом импульса, температурой и т.д.
Применимость модели материальной точки обычно формулируют в виде: «тело можно считать материальной точкой, если его размеры значительно меньше расстояний до других тел (либо меньше расстояний, на которые перемещается тело)». Эта формулировка неконкретна – не ясно, что значит «значительно меньше». Кроме того, в некоторых случаях модель материальной точки неприменима принципиально, так как она не позволяет описывать некоторые явления, связанные с конечностью размеров тела. В качестве примера материальной точки часто приводят Землю, движущуюся вокруг Солнца. Действительно, радиус Земли (R3 ≈ 6400 км) значительно меньше радиуса ее орбиты (Rорб ≈ 1,5•108 км). Однако в рамках модели нельзя описать восходы и закаты Солнца и других светил, так как модель материальной точки исключает ее вращение вокруг собственной оси. Далее, в этой модели невозможно вычислить значения приливных сил, которые тормозят ее вращение, так как эти силы прямо зависят от размеров земного шара. Таким образом, применимость этой модели не может быть сформулирована однозначно в виде малости отношения ![]() , применимость определяется и конечной целью описания.
, применимость определяется и конечной целью описания.
Говоря о вращении тела, не следует забывать, что некоторые характеристики вращательного движения можно учесть и в рамках модели материальной точки. Например, в теории идеального газа для средней кинетической энергии молекулы используют выражение ![]() , где i – число степеней свободы, в которые включают и вращательные степени свободы (для двухатомных молекул i = 5, из них 3 – поступательные, 2 – вращательные). Строго говоря, если размеры тела нулевые, то энергия вращательного движения также равна нулю (так как момент инерции равен нулю), однако можно формально не учитывать размеры молекулы, но считать, что кинетическая энергия вращательного движения отлична от нуля. Такой подход к моделированию вполне правомочен, хотя и не объясним с точки зрения физики.
, где i – число степеней свободы, в которые включают и вращательные степени свободы (для двухатомных молекул i = 5, из них 3 – поступательные, 2 – вращательные). Строго говоря, если размеры тела нулевые, то энергия вращательного движения также равна нулю (так как момент инерции равен нулю), однако можно формально не учитывать размеры молекулы, но считать, что кинетическая энергия вращательного движения отлична от нуля. Такой подход к моделированию вполне правомочен, хотя и не объясним с точки зрения физики.
Обратимся ко второму критерию применимости модели для материальной точки. Попытаемся ответить аргументировано на следующий вопрос; «Можно ли считать бегуна на стометровой дистанции материальной точкой?». (Сразу оговоримся, нас интересует чисто кинематический аспект проблемы, мы не будем затрагивать вопросы работы мышц, сопротивления воздуха, потребления кислорода и т.д.) Иными словами, «значительно ли меньше размеры бегуна, чем стометровая дистанция»?
Ответ на поставленный вопрос зависит от точности, с которой проводят измерение времени пробега. Если это время определяют с помощью ручного секундомера с погрешностью ![]() , то погрешность определения положения бегуна
, то погрешность определения положения бегуна ![]() (при скорости бега
(при скорости бега ![]() ) превосходит его поперечные размеры
) превосходит его поперечные размеры ![]() , следовательно, в этих условиях модель материальной точки вполне обоснована и применима. Если же время измеряют электронным секундомером с погрешностью
, следовательно, в этих условиях модель материальной точки вполне обоснована и применима. Если же время измеряют электронным секундомером с погрешностью ![]() , то погрешность определения положения
, то погрешность определения положения ![]() , что меньше размеров тела, поэтому считать бегуна материальной точкой нельзя – не зря на соревнованиях спринтеры на финише резко наклоняются, «бросают грудь» вперед, выигрывают победные сотые доли секунды.
, что меньше размеров тела, поэтому считать бегуна материальной точкой нельзя – не зря на соревнованиях спринтеры на финише резко наклоняются, «бросают грудь» вперед, выигрывают победные сотые доли секунды.
2. Абсолютно твердое тело – модель реального тела, изменением размеров и формы которого в данных условиях можно пренебречь.
В модели абсолютно твердого тела пренебрегают его деформациями, поэтому исчезают все эффекты, связанные с упругими свойствами тела. Так, в рамках этой модели нельзя рассчитать время соударения (даже абсолютно упругого) двух тел, скорость распространения упругих колебаний (скорость звука) в абсолютно твердом теле равна бесконечности, поэтому эта модель противоречит основным постулатам специальной теории относительности и не может в ней применяться.
Использование второго количественного критерия применимости модели абсолютно твердого тела проиллюстрируем следующим примером. Пузырек воздуха всплывает со дна озера глубиной h = 1,0 м. Можно ли при расчете времени всплытия пренебречь изменением радиуса пузырька?
Прежде всего, заметим, что глубина озера задана с точностью до двух значащих цифр, т.е. с погрешностью ![]() . Относительная погрешность этого исходного значения
. Относительная погрешность этого исходного значения ![]() , поэтому окончательный результат не может иметь более высокой точности. Всеми поправками, которые приводят к изменению времени всплытия на величину, меньшую 5%, можно пренебречь. Оценим, на сколько может измениться рассчитанное время всплытия пузырька, если учесть изменение его радиуса г при подъеме. Относительное изменение давления внутри пузырька
, поэтому окончательный результат не может иметь более высокой точности. Всеми поправками, которые приводят к изменению времени всплытия на величину, меньшую 5%, можно пренебречь. Оценим, на сколько может измениться рассчитанное время всплытия пузырька, если учесть изменение его радиуса г при подъеме. Относительное изменение давления внутри пузырька ![]() (где p – атмосферное давление,
(где p – атмосферное давление, ![]() – гидростатическое давление), таким же будет и относительное изменение объема
– гидростатическое давление), таким же будет и относительное изменение объема ![]() (лапласовским давлением пренебрегаем). Так как
(лапласовским давлением пренебрегаем). Так как ![]() , то относительное изменение радиуса
, то относительное изменение радиуса ![]() . При движении пузырька на него действует сила Архимеда и сила вязкого трения, скорость установившегося движения можно найти из условия равенства этих сил:
. При движении пузырька на него действует сила Архимеда и сила вязкого трения, скорость установившегося движения можно найти из условия равенства этих сил: ![]() (где η – вязкость воды). Следовательно, скорость движения пропорциональна квадрату радиуса
(где η – вязкость воды). Следовательно, скорость движения пропорциональна квадрату радиуса ![]() , ее изменение
, ее изменение ![]() . Если мгновенная скорость увеличивается на величину
. Если мгновенная скорость увеличивается на величину ![]() , то средняя скорость на всем интервале движения увеличивается на
, то средняя скорость на всем интервале движения увеличивается на 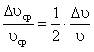 . Итого: относительное изменение времени всплытия
. Итого: относительное изменение времени всплытия 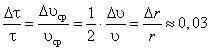 . Окончательный вывод, следующий из проведенных оценок: точность исходных данных не позволяет учесть изменение радиуса пузырька, поэтому этим изменением можно пренебречь, т.е., как это ни парадоксально, считать пузырек воздуха абсолютно твердым телом.
. Окончательный вывод, следующий из проведенных оценок: точность исходных данных не позволяет учесть изменение радиуса пузырька, поэтому этим изменением можно пренебречь, т.е., как это ни парадоксально, считать пузырек воздуха абсолютно твердым телом.
3. Идеальный газ – модель газа, в которой пренебрегают собственными размерами молекул и дистанционным взаимодействием между ними. Обычно в учебниках утверждают, что эта модель хорошо описывает свойства реального газа при низких давлениях и плотностях и высоких температурах. Чтобы провести количественные оценки применимости модели идеального газа, необходимо сравнить уравнение состояния Менделеева-Клапейрона с более точным уравнением состояния, например, уравнением Ван-дер-Ваальса.
Оценим поправки к изменению давления, вызванные учетом размеров молекул и их взаимного притяжения.
Из уравнения Ван-дер-Ваальса (для одного моля) ![]() найдем
найдем ![]() , где a, b – поправки Ван-дер-Ваальса. Таким образом, оценка погрешности модели идеального газа
, где a, b – поправки Ван-дер-Ваальса. Таким образом, оценка погрешности модели идеального газа ![]() может быть получена численно, затем ее следует сравнить с требуемой точностью расчетов и сделать окончательный обоснованный вывод о применимости модели.
может быть получена численно, затем ее следует сравнить с требуемой точностью расчетов и сделать окончательный обоснованный вывод о применимости модели.
Отметим, что модель Ван-дер-Ваальса, помимо повышения точности, предсказывает и качественно описывает фазовый переход газ – жидкость, который принципиально отсутствует в модели идеального газа. Поэтому при описании процесса конденсации модель идеального газа неприменима.
4. Точечный заряд – модель заряженного тела, размерами которого в данных условиях можно пренебречь.
Эта модель физически внутренне противоречива, так как точечный заряд обладает бесконечной энергией[*], но тем не менее широко применяется в физике. Оценим, каковы должны быть размеры тела, чтобы ими можно было пренебречь. Как всегда, ответ зависит от цели исследования и от требуемой точности. Пусть нам необходимо рассчитать напряженность электростатического поля в точке, находящейся на расстоянии l от заряженного тела, размер которого d. Для оценки примем, что тело представляет собой две одинаково заряженные материальные точки, находящиеся на расстоянии d друг от друга. Если пренебречь расстоянием между точками (d « l), то напряженность электростатического поля Ε определяется выражением ![]() .
.
Напряженность поля, создаваемого двумя точечными зарядами q, находящимися на расстоянии d друг от друга, будет
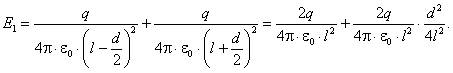
Таким образом, погрешность, возникающая из-за пренебрежения размерами тела, может быть оценена 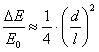 . Если, например, необходимо рассчитать напряженность с точностью η = 1%, то при l > 5d можно считать заряженное тело точечным, т.е. на расстояниях, более чем в 5 раз превышающих размеры тела, тело можно считать точечным.
. Если, например, необходимо рассчитать напряженность с точностью η = 1%, то при l > 5d можно считать заряженное тело точечным, т.е. на расстояниях, более чем в 5 раз превышающих размеры тела, тело можно считать точечным.
Рассмотрим еще один пример на эту тему. Допустим, заряженное тело является проводником. При его взаимодействии с другим зарядом на проводнике возникают индуцированные заряды. В модели точечного заряда ни о каких индуцированных зарядах не может быть и речи – они принципиально отсутствуют. Проведем оценки, при каких условиях можно пренебречь индуцированными зарядами, т.е. опять воспользоваться моделью точечного заряда. Пусть изолированный металлический шар радиусом R и несущий заряд Q взаимодействуют с точечным зарядом q, находящимся на расстоянии r от центра шара. Если пренебречь перераспределением заряда на поверхности шара вследствие электростатической индукции, то сила взаимодействия между телами может быть найдена из закона Кулона: ![]() .
.
Вследствие электростатической индукции распределение заряда по поверхности шара изменится – это изменение приведет к изменению поля, создаваемого шаром. Последнее в свою очередь может быть описано (см., например, [1]) как поле, создаваемое точечным зарядом ![]() , находящимся на расстоянии
, находящимся на расстоянии ![]() от центра шара, и зарядом
от центра шара, и зарядом ![]() , расположенным в центре шара. Следовательно, изменение силы взаимодействия шара с точечным зарядом можно найти по формуле
, расположенным в центре шара. Следовательно, изменение силы взаимодействия шара с точечным зарядом можно найти по формуле
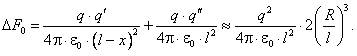
Относительная погрешность моделирования шара точечным зарядом 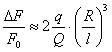 зависит не только от отношения
зависит не только от отношения ![]() , но и от отношения зарядов
, но и от отношения зарядов ![]() . Пусть, например, q = Q, а допустимая погрешность расчета силы взаимодействия η = 1%. Тогда можно «забыть» о размерах шара при
. Пусть, например, q = Q, а допустимая погрешность расчета силы взаимодействия η = 1%. Тогда можно «забыть» о размерах шара при 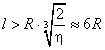 . При меньших расстояниях необходимо учитывать индуцированные заряды, тем более, возможно, что сила отталкивания между одноименно заряженными телами сменится силой притяжения. Два одноименно заряженных тела (но не точечных!) могут притягиваться! Описать (и даже предсказать) такой эффект в модели точечных зарядов нельзя, что, естественно, накладывает ограничения на применимость этой модели.
. При меньших расстояниях необходимо учитывать индуцированные заряды, тем более, возможно, что сила отталкивания между одноименно заряженными телами сменится силой притяжения. Два одноименно заряженных тела (но не точечных!) могут притягиваться! Описать (и даже предсказать) такой эффект в модели точечных зарядов нельзя, что, естественно, накладывает ограничения на применимость этой модели.
Перейдем к рассмотрению моделей некоторых физических явлений с тех же позиций сформулированных ранее критериев.
5. «Сопротивлением воздуха пренебречь.» Эта фраза очень часто встречается во всевозможных сборниках физических задач. Пренебрежение сопротивлением воздуха является, конечно, одним из этапов построения модели движения. В рамках такой модели исчезают всевозможные «красивые» эффекты – подъемная сила крыла, замысловатые крученые удары, «кружева» падающих листьев и т.д. Учет сопротивления воздуха приводит к более простым, но не менее странным, вторичным эффектам. Так, например, максимальная дальность полета достигается при углах вылета, меньших 45°, причем, чем больше начальная скорость, тем меньше должен быть угол бросания [2].
Построим теперь количественные оценки, позволяющие сформулировать четкие условия возможности пренебрежения сопротивлением воздуха. Можно показать, что при квадратичной зависимости силы сопротивления от скорости поправка к времени падения, связанная с учетом сил сопротивления, имеет вид 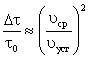 , где υcp – средняя скорость движения тела, υуст – скорость установившегося движения в поле тяжести. Так, например, скорость установившегося движения при падении человека в воздухе
, где υcp – средняя скорость движения тела, υуст – скорость установившегося движения в поле тяжести. Так, например, скорость установившегося движения при падении человека в воздухе ![]() [3]. Если допустимая погрешность расчета времени падения η = 1%, то при
[3]. Если допустимая погрешность расчета времени падения η = 1%, то при ![]() оценка высоты, при которой можно использовать рассматриваемую модель, имеет вид
оценка высоты, при которой можно использовать рассматриваемую модель, имеет вид 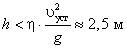 , при больших высотах учет сопротивления воздуха необходим.
, при больших высотах учет сопротивления воздуха необходим.
6. Малые колебания математического маятника. Известна формула для вычисления периода малых колебаний математического маятника. Однако что такое «малые» колебания? Ответ, как всегда, зависит от точности, с которой необходимо вычислить (или измерить экспериментально) период. Если амплитуда колебаний равна φ0 радиан, то период колебаний (см., например, [4]) 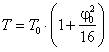 . Следовательно, при максимально допустимой относительной погрешности определения периода η малыми будут колебания, амплитуда которых
. Следовательно, при максимально допустимой относительной погрешности определения периода η малыми будут колебания, амплитуда которых ![]() . Так, при η = 1%
. Так, при η = 1% ![]() , т.е. колебания с амплитудой 20° являются малыми. Если же погрешность измерения η = 10%, то «малыми» будут колебания с амплитудой φ0 = 70°.
, т.е. колебания с амплитудой 20° являются малыми. Если же погрешность измерения η = 10%, то «малыми» будут колебания с амплитудой φ0 = 70°.
7. Изотермический процесс. Все процессы идеального газа, рассматриваемые в школьном курсе физики, – изотермический, изобарный, изохорный, адиабатный – являются модельными, идеальными, так как абсолютно точно не могут быть воспроизведены практически. Любой реальный процесс является неравновесным, так как в каждой системе состояние равновесия устанавливается только через какой-то конечный интервал времени (времени релаксации). Однако использование моделей равновесных процессов позволяет достаточно просто рассчитать характеристики процесса и при необходимости оценить погрешности моделирования.
Остановимся немного подробнее на анализе модели изотермического процесса. Главная особенность этого процесса, с моей точки зрения, заключается в том, что он внутренне противоречив. Покажем это на примере изучения цикла Карно. Рабочее тело приводится в контакт с нагревателем, получает от него теплоту при изотермическом расширении, после адиабатного расширения температура рабочего тела становится равной температуре холодильника, затем при изотермическом процессе рабочее тело отдает теплоту холодильнику. А теперь зададимся вопросом: «Почему, когда температура тела равна температуре нагревателя, теплота передается от нагревателя к рабочему телу, а когда температура тела равна температуре холодильника, теплота передается от рабочего тела к холодильнику?». Ответить на этот вопрос невозможно. Для того чтобы существовал поток теплоты, необходима разность температур. Следовательно, в первом случае температура рабочего тела должна быть немного меньше температуры нагревателя, а во втором чуть-чуть больше температуры холодильника. Таким образом, в этой модели мы пренебрегаем фактором (разностью температур), оказывающим очень слабое влияние на расчет параметров процесса, но без которого сам процесс осуществляться не может, фактором, который определяет направление процесса.
8. Квазистационарный электрический ток. Проблема, аналогичная рассмотренной выше, может возникнуть и при изучении переменных токов. Например, основное уравнение, описывающее процессы в идеальном колебательном контуре (т.е. без электрического сопротивления), имеет смысл равенства ЭДС самоиндукции в катушке и напряжения на конденсаторе. Тогда почему же на одном из этапов конденсатор заряжается, а на другом разряжается? Очевидно, что в процессе зарядка ЭДС самоиндукции чуть больше напряжения на конденсаторе, а в ходе разрядки – чуть меньше. Опять мы встречаемся с моделью, в которой пренебрегают фактором, фактически обеспечивающим протекание описываемых процессов. В этом примере необходимую малую разность обеспечивает неизбежное электрическое сопротивление контура.
Рассмотрим более сложную задачу: «Сверхпроводящее кольцо радиусом R с индуктивностью L помещено в магнитное поле, индукция которого возрастает от 0 до В. Считая, что вектор индукции перпендикулярен плоскости кольца, найдите силу тока в кольце».
формальное решение этой задачи не сложно: так как сопротивление кольца равно нулю, то в любой момент времени ЭДС индукции равна ЭДС самоиндукции: ![]() , отсюда
, отсюда ![]() .
.
Снова мы сталкиваемся с проблемой физического истолкования явления: почему в кольце ток возрастает, если суммарная ЭДС равна нулю? Опять необходимо искать причину, обеспечивающую малую разность между ЭДС индукции и ЭДС самоиндукции. В данном случае таким фактором служит инерционность электронов (т.е. их масса). Более строгое решение этой задачи (см. [5]) с учетом массы электронов приводит к ответу, отличающемуся от приведенного весьма незначительно. Поэтому можно считать это решение верным, но физическая сущность процессов возникновения тока в нем исчезла.
9. Идеальные измерительные приборы. Описание измерений физических величин во многих случаях также является модельным. В ходе обработки результатов измерений приходится делать всевозможные допущения, приближения, следовательно, необходим анализ допустимости этих приближений. Эта проблема требует обсуждения и с методической точки зрения: мысль о том, что всякое измерение есть вмешательство в ход исследуемого явления, имеет принципиальное значение в физике микромира. Однако она может быть проиллюстрирована и в классической физике.
Измеряя силу тока в цепи с помощью амперметра, часто не учитывают влияния сопротивления амперметра на величину тока. Измеряя температуру с помощью термометра, пренебрегают теплоемкостью термометра и т.д. Не составляет большого труда учесть поправки, связанные с «вмешательством» приборов, и сформулировать условия, при которых ими можно пренебречь. Рассмотрим, для примера, условия, при которых можно пренебречь влиянием амперметра на величину силы тока в цепи. По закону Ома сила тока в контуре ![]() , где R – полное сопротивление контура, RA – сопротивление амперметра. Считая
, где R – полное сопротивление контура, RA – сопротивление амперметра. Считая ![]() , получим
, получим ![]() или относительную погрешность, вносимую амперметром. Если измерения проводятся с помощью стандартного школьного амперметра, приборная погрешность которого ~ 4%, то при
или относительную погрешность, вносимую амперметром. Если измерения проводятся с помощью стандартного школьного амперметра, приборная погрешность которого ~ 4%, то при ![]() изменение тока, вызванное включением амперметра, меньше погрешности прибора, поэтому в этом случае амперметр можно считать идеальным.
изменение тока, вызванное включением амперметра, меньше погрешности прибора, поэтому в этом случае амперметр можно считать идеальным.
Заключение. Рассмотренные примеры показывают, что анализ применимости различных физических моделей необходим, его проведение можно осуществить вполне доступными для школьников методами. Главная методическая ценность анализа адекватности модели заключается в том, что он требует выхода за рамки данной модели (перехода к более сложной другой модели), тем самым демонстрирует ограниченность физических теорий и бесконечность процесса познания.
1. Слободянюк А. Метод изображений в электростатике // Фокус. – 1994. – №2. – С. 63-71.
2. Слободянюк А. Сопротивление воздуха не учитывать... // Фокус. – 1995. – №1. – С. 41-51.
3. Матвеев Α.Η. Механика и теория относительности. – М.: Высш. школа, 1976.
4. Слободянюк А. Математический маятник: что такое «малые» колебания? // Фокус. – 1994. – №3. – С. 53-57.
5. Слободянюк А. Закон Ома // Фокус. – 1993. – №3. – С. 28-35.
[*]Эта проблема не нашла еще решения в современной физике. Так, до сих пор нет экспериментальных данных, которые свидетельствовали бы о наличии размеров электрона, т.е. во всех экспериментах электрон ведет себя как точечная частица.
| Выложил | alsak |
| Опубликовано | 27.12.07 |
| Просмотров | 10622 |
| Рубрика | Решение задач |
| Тема | Без тем |