Овчинников А., Плис В. Законы сохранения в задачах на столкновения // Квант
Овчинников А., Плис В. Законы сохранения в задачах на столкновения // Квант. — 2001. — № 1. — С. 43-45.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Происходящие в обычных условиях столкновения обычных тел почти всегда бывают в той или иной степени неупругими — уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т.е. переходом части их кинетической энергии в тепло. Тем не менее, в физике понятие об упругих столкновениях играет важную роль. В частности, с такими столкновениями приходится иметь дело в физическом эксперименте в области атомных явлений.
Обсудим несколько конкретных задач.
Задача 1. Протон, пролетая мимо первоначально покоившегося ядра неизвестного химического элемента, отклонился на угол β = arccos (4/15), а величина скорости протона уменьшилась на 10% (рис. 1). Найдите массовое число химического элемента.
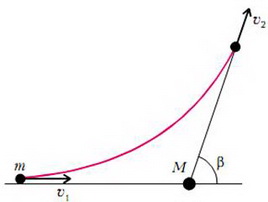
Рис. 1
Взаимодействие частиц упругое; следовательно, импульс и энергия системы сохраняются:
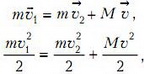
где m1, υ1 и υ2 — масса и скорости протона, М и υ — масса и скорость неизвестного ядра. Из закона сохранения импульса с помощью теоремы косинусов получаем
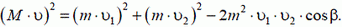
Из двух последних соотношений получаем искомое массовое число:
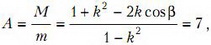
где ![]() .
.
Следовательно, протон столкнулся с ядром лития.
Задача 2. Каков максимальный угол β упругого рассеяния α-частицы в водороде? Масса атома водорода в 4 раза меньше массы α-частицы.
Первый способ решения. Проанализируем упругое столкновение в лабораторной (неподвижной) системе отсчета. Введем обозначения: m1 — масса α-частицы, ![]() — ее скорость до рассеяния, m2 — масса атома водорода,
— ее скорость до рассеяния, m2 — масса атома водорода, 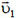 и
и 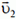 — скорости α-частицы и атома водорода, соответственно, после рассеяния.
— скорости α-частицы и атома водорода, соответственно, после рассеяния.
Взаимодействие упругое; следовательно, сохраняются импульс (рис. 2) и кинетическая энергия системы α-частица — атом водорода:
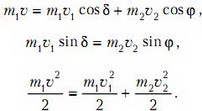
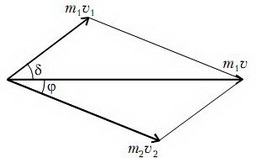
Рис. 2
Исключив из этих соотношений угол φ и скорость υ2, получим относительно υ1 квадратное уравнение
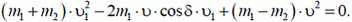
Корни этого уравнения будут вещественными при ![]() . Максимальный угол δ, удовлетворяющий этому условию, и есть искомый угол θ. Таким образом,
. Максимальный угол δ, удовлетворяющий этому условию, и есть искомый угол θ. Таким образом,
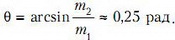
Заметим, что рассеяние на максимальный угол возможно только при условии, что масса налетающей частицы больше массы покоящейся.
Второй способ решения. В общем случае столкновение удобно рассматривать в системе центра масс сталкивающихся частиц (в системе, где их суммарный импульс равен нулю). Скорость центра масс нашей системы тел равна
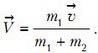
До столкновения импульс частицы массой m1, равен
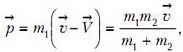
а импульс частицы массой m2 равен 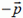 .
.
При упругом столкновении импульс и энергия взаимодействующей системы тел сохраняются. Так что если импульс первой частицы после столкновения обозначить 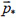 , то импульс второй будет
, то импульс второй будет 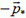 . Из закона сохранения энергии, записанном в виде
. Из закона сохранения энергии, записанном в виде
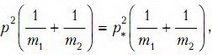
находим
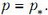
Таким образом, единственное, что происходит в рассматриваемой системе при столкновении, это поворот импульсов частиц, т.е. изменение их направления без изменения величины. Вместе с импульсами так же изменяются и скорости обеих частиц. Угол поворота зависит от конкретного характера взаимодействия частиц и от их взаимного расположения при столкновении.
При переходе в лабораторную систему отсчета воспользуемся правилом сложения скоростей. В соответствии с ним, скорость налетающей частицы после столкновения равна
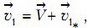
где 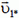 — ее скорость в системе центра масс. На рисунке 3 из одной точки отложены векторы
— ее скорость в системе центра масс. На рисунке 3 из одной точки отложены векторы ![]() — скорость центра масс системы и
— скорость центра масс системы и ![]() — скорость налетающей частицы до столкновения.
— скорость налетающей частицы до столкновения.
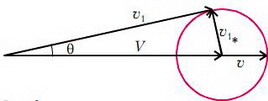
Рис. 3
Величина
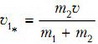
определяет радиус окружности, на которой заканчивается вектор 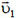 . Из рисунка следует, что в случае m1 > m2 угол между векторами скоростей
. Из рисунка следует, что в случае m1 > m2 угол между векторами скоростей ![]() и
и 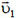 налетающей частицы до и после столкновения не может превышать некоторого максимального значения θ, соответствующего случаю, когда
налетающей частицы до и после столкновения не может превышать некоторого максимального значения θ, соответствующего случаю, когда  касается окружности, т.е.
касается окружности, т.е.
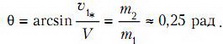
Задача 3. Первая искусственная ядерная реакция наблюдалась Резерфордом в 1919 году. Она идет с поглощением энергии Q = 1,13 МэВ. Какую минимальную кинетическую энергию Епор следует сообщить в лабораторной системе отсчета α-частице, чтобы при бомбардировке неподвижной мишени из азота указанная реакция могла произойти?
Пороговой энергией Епор, или порогом ядерной реакции, называют такую энергию налетающей на неподвижную мишень частицы, начиная с которой ядерная реакция становится возможной.
Сначала — небольшое отступление. Найдем связь кинетических энергий Ек и Ек* системы материальных точек в лабораторной системе отсчета и в системе центра масс соответственно. По закону сложения скоростей, для каждой i-й материальной точки
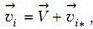
где ![]() — скорость центра масс системы. Тогда кинетическая энергия системы материальных точек в лабораторной системе равна
— скорость центра масс системы. Тогда кинетическая энергия системы материальных точек в лабораторной системе равна
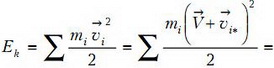
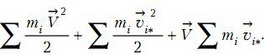
Сумма 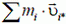 равна нулю, так как она определяет скорость центра масс в системе центра масс. Таким образом,
равна нулю, так как она определяет скорость центра масс в системе центра масс. Таким образом,
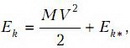
т.е. кинетическая энергия совокупности материальных точек в лабораторной системе отсчета равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и кинетической энергии той же совокупности материальных точек в ее относительном движении в системе центра масс.
Теперь приступим к решению задачи. Обозначим через 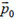 импульс α-частицы до столкновения. Кинетическая энергия движения центра масс системы
импульс α-частицы до столкновения. Кинетическая энергия движения центра масс системы
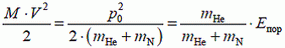
не изменяется при ядерной реакции, так как импульс замкнутой системы сохраняется и поэтому указанная энергия не участвует в ядерных превращениях. Тогда искомую энергию найдем из условия
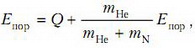
откуда
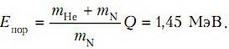
Заметим, что минимум кинетической энергии бомбардирующей частицы достигается в случае, когда продукты реакции покоятся в системе центра масс.
Задача 4. Неподвижный невозбужденный атом водорода поглощает фотон. В результате атом переходит в возбужденное состояние и начинает двигаться. Найдите величину υ скорости, с которой стал двигаться атом после поглощения фотона. Энергия возбуждения атома водорода E12 = 1,63·10–18 Дж, энергия покоя ![]() = 1,49·10–10 Дж.
= 1,49·10–10 Дж.
Указание. При ![]() можно считать, что
можно считать, что 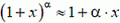 .
.
Первый способ решения. Поглощение фотона атомом является типичным неупругим столкновением. Из законов сохранения энергии:
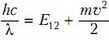
и импульса:
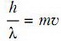
находим искомую скорость:
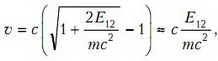
которая определяется только отношением энергии возбуждения к энергии покоя атома водорода. При выводе учтено, что в числителе стоит величина, на много порядков меньшая, чем в знаменателе. Это подтверждает нерелятивистское приближение, использованное в решении.
Итак, при переходе атома водорода из основного состояния в первое возбужденное состояние атом начинает двигаться со скоростью
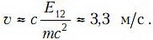
Второй способ решения. При записи законов сохранения энергии и импульса воспользуемся релятивистскими формулами для энергии и импульса:
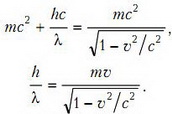
Далее, разделим второе соотношение на первое и получим
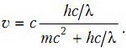
Энергия поглощаемого фотона много меньше энергии покоя атома, поэтому выражение можно представить в виде
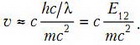
Задача 5. На неподвижный невозбужденный атом водорода налетает другой невозбужденный атом водорода. Какова минимальная кинетическая энергия налетающего атома, при которой в результате столкновения может излучиться фотон? Энергия ионизации атома водорода 13,6 эВ.
Налетающий атом передаст на ионизацию максимально возможную энергию при таком неупругом столкновении, когда оба атома в системе центра масс будут покоиться. Кинетическая энергия движения центра масс системы, равная
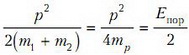
(где mр — масса протона, а Епор — пороговая энергия), не изменяется при ядерной реакции, так как импульс замкнутой системы сохраняется и поэтому указанная энергия не участвует в ядерных превращениях. Фотон унесет минимальную энергию, если электрон в атоме водорода перейдет с первого уровня на второй. Для этого атом должен поглотить энергию
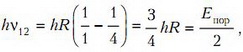
где R — постоянная Ридберга. При ионизации электрон переходит с первого уровня на бесконечность; следовательно, энергия ионизации
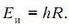
Из полученных соотношений находим
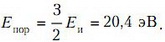
Задача 6. Рентгеновский фотон сталкивается с неподвижным электроном и отражается в обратном направлении. Найдите приращение длины волны фотона в результате рассеяния.
При энергиях в сотни тысяч электрон-вольт необходим учет релятивистских эффектов. Законы сохранения энергии и импульса принимают вид
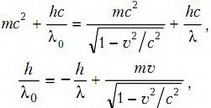
где m — масса электрона, λ0 и λ — длины волн фотона. Умножим второе равенство на с, сложим его с первым и вычтем его из первого равенства. Перемножив полученные соотношения, найдем
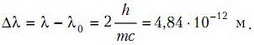
Заметим, что это вполне согласуется с экспериментальными данными.
Упражнения
1. Ядро лития возбуждается пучком протонов, падающим на неподвижную литиевую мишень. При этом происходит реакция
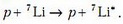
При каких отношениях энергии налетающего протона к энергии возбуждения лития возможно возникновение протонов, движущихся в обратном к потоку направлении?
2. На неподвижный невозбужденный атом водорода налетает электрон. Какова минимальная кинетическая энергия Епор налетающего электрона, при которой в результате столкновения может излучаться фотон? Энергия ионизации атома водорода Еи = 13,6 эВ.
3. Рентгеновский фотон сталкивается с неподвижным электроном и отражается в перпендикулярном направлении. Найдите приращение длины волны фотона в результате рассеяния.
Ответы
1. 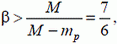 где М — масса ядра лития, а mр — масса протона.
где М — масса ядра лития, а mр — масса протона.
2. 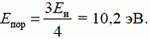
3. 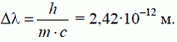
| Выложил | alsak |
| Опубликовано | 14.05.09 |
| Просмотров | 17653 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |