Черноуцан А.И. Законы сохранения энергии и импульса // Квант
Черноуцан А.И. Законы сохранения энергии и импульса // Квант. — 1989. — № 4. — С. 60-64.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье обсуждается вопрос совместного использования двух законов сохранения — энергии и импульса — для решения различных физических задач.
На приемных экзаменах по физике нередко возникает ситуация, когда абитуриенты, хорошо зная каждый закон сохранения в отдельности, испытывают «психологические» трудности при необходимости соединить эти законы вместе, в рамках одной задачи. Причем чаще всего от внимания ускользает более простой, на наш взгляд, закон — закон сохранения импульса. Записав соответствующее уравнение для энергии, абитуриент уже не вспоминает об импульсе — и ... попадает впросак. Впрочем, бывает и по-другому.
Рассмотрим несколько конкретных примеров того, как именно совместные «усилия» энергии и импульса приводят к нужному результату.
Задача 1. Два шарика, сделанные из одного материала и имеющие массы m1 и m2, движутся навстречу друг другу со скоростями υ1 и υ2. На сколько возрастет температура шариков после лобового абсолютно неупругого удара, если удельная теплоемкость материала шариков с? Начальные температуры шариков были одинаковыми.
Изменение температуры шариков определяется увеличением их внутренней энергии:
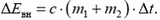
Многие абитуриенты ошибочно считают, что в результате удара во внутреннюю энергию переходит вся начальная кинетическая энергия системы 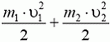 . При этом они забывают, что шарики не могут остановиться после удара, так как это противоречило бы закону сохранения импульса — начальный импульс системы
. При этом они забывают, что шарики не могут остановиться после удара, так как это противоречило бы закону сохранения импульса — начальный импульс системы 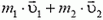 , вообще говоря, не равен нулю. Значит, при подсчете энергии надо учесть и кинетическую энергию шариков в конечном состоянии.
, вообще говоря, не равен нулю. Значит, при подсчете энергии надо учесть и кинетическую энергию шариков в конечном состоянии.
Обозначим скорость слипшихся после абсолютно неупругого удара шариков через υ и запишем законы сохранения энергии и импульса, точнее — проекции импульса на направление движения первого шарика:
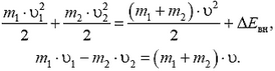
Решая совместно полученные три уравнения, находим искомое увеличение температуры:
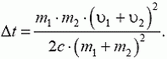
Задача 2. Два вагона, массы которых М1 и М2, движутся навстречу друг другу со скоростями υ1 и υ2. При столкновении происходит сжатие четырех одинаковых буферных пружин, после чего вагоны расходятся. Найдите максимальную деформацию каждой пружины, если ее жесткость равна k.
В этой задаче, в отличие от предыдущей, можно использовать закон сохранения механической энергии (подразумевается, что трение мало, а пружины идеальные), приравняв начальную энергию вагонов к энергии системы в тот момент, когда деформация пружин х максимальна. При этом искомая величина х войдет в потенциальную энергию упругой деформации пружин:
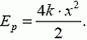
Однако, кроме этой энергии, надо учесть еще и кинетическую энергию вагонов.
Тот факт, что при максимальном сближении вагоны не останавливаются (о чем, к сожалению, забывают многие абитуриенты), следует, как и в предыдущей задаче, из закона сохранения импульса. Единственная особенность этого момента состоит в том, что при максимальной деформации пружин скорости вагонов одинаковы: 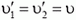 . Поэтому законы сохранения энергии и импульса (вернее — его проекции) выглядят следующим образом:
. Поэтому законы сохранения энергии и импульса (вернее — его проекции) выглядят следующим образом:
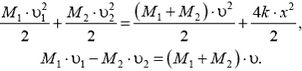
Отсюда получаем
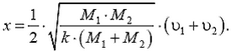
Задача 3 (баллистический маятник). В брусок массой М, висящий на параллельных нитях длиной L, попадает горизонтально летящая пуля массой m и застревает в нем (рис. 1). В результате удара каждая нить отклоняется на угол α. Найдите начальную скорость пули υ. Нити считать идеальными (невесомыми и нерастяжимыми).
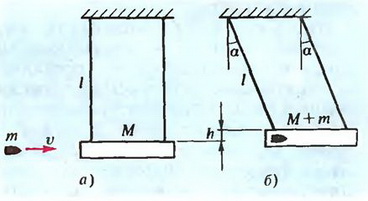
Рис. 1.
Как видно из рисунка, угол отклонения нитей α связан с высотой h, на которую поднимается брусок:
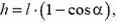
а высоту h можно связать с потенциальной энергией бруска и пули в конечном состоянии:
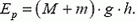
Возникает вопрос: выполняется ли в данной ситуации закон сохранения механической энергии? Другими словами, равна ли энергия системы в конечном состоянии ее начальной энергии, т. е. кинетической энергии пули 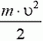 . Ответ, конечно, отрицательный. Ведь мы знаем, что при неупругом ударе часть механической энергии переходит во внутреннюю. Как же быть? Рассмотрим еще одно, промежуточное состояние системы — сразу после окончания удара, когда пуля уже застряла в бруске, но нити еще вертикальны. Энергия системы в этом состоянии представляет собой просто кинетическую энергию бруска с пулей:
. Ответ, конечно, отрицательный. Ведь мы знаем, что при неупругом ударе часть механической энергии переходит во внутреннюю. Как же быть? Рассмотрим еще одно, промежуточное состояние системы — сразу после окончания удара, когда пуля уже застряла в бруске, но нити еще вертикальны. Энергия системы в этом состоянии представляет собой просто кинетическую энергию бруска с пулей: 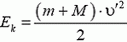 , где υ´ — их общая скорость. После того как неупругий удар уже закончился, энергия больше теряться не будет, и можно записать
, где υ´ — их общая скорость. После того как неупругий удар уже закончился, энергия больше теряться не будет, и можно записать
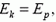
или
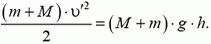
Скорость υ´ можно связать с начальной скоростью пули с помощью закона сохранения импульса
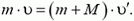
Из последних двух уравнений, с учетом выражения для h, имеем
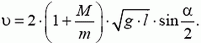
Заметим, что в этой задаче законы сохранения импульса и энергии работают не одновременно, а как бы по очереди. Понять это оказывается не так просто, и многие абитуриенты решают задачи такого типа с помощью одного закона сохранения энергии, получая, конечно же, неправильные результаты.
Задача 4. Три маленьких заряженных шарика — масса каждого шарика m, заряд q — соединены одинаковыми идеальными нитями длиной l и образуют равносторонний треугольник (рис. 2). Одну из нитей перерезают, и шарики приходят в движение. Найдите максимальную скорость среднего шарика (3) в процессе движения. Действием сил тяготения можно пренебречь.
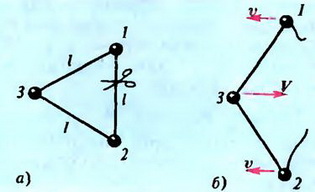
Рис. 2.
Так как система замкнута и в ней действуют только силы кулоновского взаимодействия, к системе можно применить закон сохранения энергии. При этом энергию взаимодействия шариков 1, 3 и 2, 3 учитывать не будем, поскольку она в состояниях а) и б) (см. рис. 2) одна и та же. Тогда закон сохранения энергии будет иметь вид
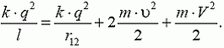
На основании одного этого уравнения нельзя не только вычислить искомую скорость V, но и понять, когда она максимальна. Однако раз система замкнута, мы можем применить еще и закон сохранения импульса — полный импульс трех шариков все время равен нулю. Для проекций импульсов получим
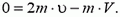
Теперь видно, что скорость V будет максимальной при наибольшем удалении шариков 1 и 2 друг от друга, т. е. когда 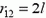 . Решая соответствующие уравнения, найдем
. Решая соответствующие уравнения, найдем
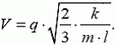
Почему-то многим школьникам использование при решении этой задачи закона сохранения импульса кажется необычным или даже странным.
Задача 5. На бруске длиной l и массой М, расположенном на гладкой горизонтальной поверхности, лежит маленькое тело массой m (рис. 3). Коэффициент трения между телом и бруском μ. С какой скоростью υ должна двигаться система, чтобы после упругого удара бруска о стенку тело упало с бруска?
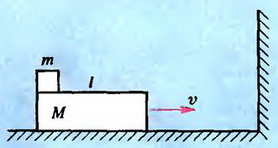
Рис. 3.
Удар бруска о стенку приведет к тому, что его скорость скачком изменится на противоположную. Скорость же тела за время удара измениться не успеет, и оно начнет скользить по бруску.
Найдем, на какое расстояние х переместится тело относительно бруска до окончания скольжения. Ясно, что условие х > l и будет условием падения тела с бруска. С расстоянием х связана работа силы трения скольжения —
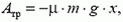
которая, в свою очередь, равна изменению кинетической энергии системы:
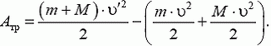
Здесь υ´ — скорость бруска с телом в тот момент, когда тело останавливается относительно бруска. Эту скорость можно найти из закона сохранения импульса
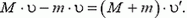
Решая совместно все три уравнения, получаем
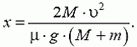
Условие х > l позволяет найти искомую скорость:
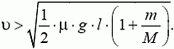
Может показаться непонятным, почему работа Атр равна произведению силы на перемещение тела относительно бруска — ведь брусок не стоит на месте, а значит, перемещение тела относительно земли не равно его перемещению относительно бруска. Дело в том, что изменение механической энергии системы равно полной работе Fтp — как над телом, так и над бруском:
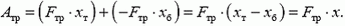
В заключение разберем задачу на расчет ядерной реакции. В этой задаче более отчетливо, чем в предыдущих, выступает векторный характер закона сохранения импульса.
Задача 6. Для проведения реакции синтеза тяжелого и сверхтяжелого изотопов водорода 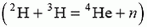 ускоренные до энергии Е = 2 МэВ ядра дейтерия направляют на тритиевую мишень. Детектор регистрирует нейтроны, вылетающие перпендикулярно направлению пучка дейтронов. Определите энергию регистрируемых нейтронов, если в реакции выделяется энергия ΔЕ = 14 МэВ.
ускоренные до энергии Е = 2 МэВ ядра дейтерия направляют на тритиевую мишень. Детектор регистрирует нейтроны, вылетающие перпендикулярно направлению пучка дейтронов. Определите энергию регистрируемых нейтронов, если в реакции выделяется энергия ΔЕ = 14 МэВ.
Закон сохранения энергии в этой реакции имеет вид
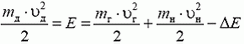
(здесь и далее индекс «д» обозначает дейтерий, «г» — гелий, «н» — нейтрон). Закон сохранения импульса надо записать в проекциях как на ось X (направление скорости падающих дейтронов), так и на ось Y (направление вылета регистрируемых нейтронов):
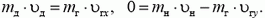
Принимая во внимание, что 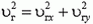 , получаем
, получаем
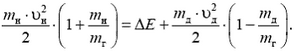
Отсюда, учитывая, что 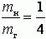 , а
, а 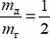 , находим энергию регистрируемых нейтронов:
, находим энергию регистрируемых нейтронов:
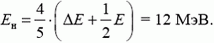
Упражнения
1. Тележка массой М движется со скоростью υ по гладкой горизонтальной поверхности (рис. 4). На тележку с высоты Н падает кирпич и остается на тележке. Какое количество теплоты выделится при ударе? Масса кирпича m.
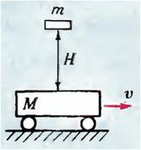
Рис. 4.
2. Ядро, летевшее со скоростью 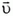 , в результате ядерной реакции разлетается на два осколка. Массы осколков m1 и m2, а их скорости
, в результате ядерной реакции разлетается на два осколка. Массы осколков m1 и m2, а их скорости 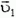 и
и 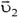 составляют между собой угол α. Какая энергия выделяется в этой реакции?
составляют между собой угол α. Какая энергия выделяется в этой реакции?
3. Брусок массой М, лежащий на гладкой горизонтальной поверхности, прикреплен к вертикальной стене пружиной жесткости k. В брусок попадает горизонтально летящая пуля и застревает в нем. Найдите максимальную деформацию пружины. Масса пули m, ее скорость υ.
4. На гладкой горизонтальной плоскости стоит клин массой М (рис. 5). На клин въезжает тело массой m, двигавшееся по плоскости со скоростью υ. На какую максимальную высоту поднимется тело по клину? Нижняя часть клина имеет плавное соединение с плоскостью.

Рис. 5.
5. На тележке укреплен штатив, к которому с помощью нити прикреплен шарик (рис. 6). Сначала нить с шариком удерживают под углом α к вертикали, а потом отпускают. Найдите максимальную скорость, приобретаемую тележкой. Масса тележки со штативом М, масса шарика m, длина нити l. Тележка находится на гладкой горизонтальной плоскости.
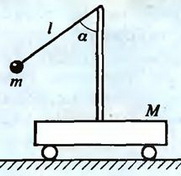
Рис. 6.
Ответы
1. 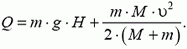
2. 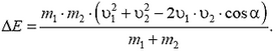
3. 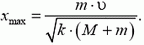
4. 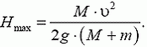
5. 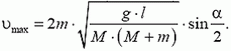
| Выложил | alsak |
| Опубликовано | 09.05.09 |
| Просмотров | 25420 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |