Зайцев И.А. Работа, мощность, энергия // Квант
Зайцев И.А. Работа, мощность, энергия // Квант. — 1972. — № 10. — С. 52-58.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Если на движущееся тело действует постоянная сила  под углом α к направлению перемещения
под углом α к направлению перемещения 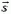 (рис. 1), то эта сила совершает работу
(рис. 1), то эта сила совершает работу
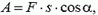 (1)
(1)
где F и s — модули векторов  и
и 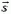 .
.
Работа силы равна произведению модулей векторов силы и перемещения тела на косинус угла между ними.
Рассмотрим подробно эту хорошо известную формулу. Если угол 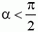 , то cos α > 0 и работа силы положительна. При
, то cos α > 0 и работа силы положительна. При 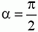 , то есть когда сила
, то есть когда сила  перпендикулярна перемещению тела
перпендикулярна перемещению тела 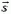 , работа, совершенная силой
, работа, совершенная силой  , равна нулю. (В частности, равна нулю работа силы, сообщающей телу центростремительное ускорение. При равномерном движении тела по окружности сила, действующая на него, перпендикулярна скорости тела.) Если
, равна нулю. (В частности, равна нулю работа силы, сообщающей телу центростремительное ускорение. При равномерном движении тела по окружности сила, действующая на него, перпендикулярна скорости тела.) Если 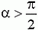 , то cos α < 0 и работа силы отрицательна. Разберемся, что это означает.
, то cos α < 0 и работа силы отрицательна. Разберемся, что это означает.
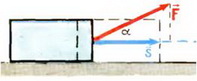
Рис. 1.
Возьмем простой случай, когда сила  параллельна вектору перемещения тела. В этом случае тело движется с ускорением
параллельна вектору перемещения тела. В этом случае тело движется с ускорением 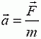 , направление которого совпадает с направлением вектора силы.
, направление которого совпадает с направлением вектора силы.
Если направление вектора силы совпадает с направлением перемещения тела, то скорость тела увеличивается, а сила  совершает положительную работу. Если же вектор силы направлен противоположно вектору перемещения тела, то ускорение тела направлено противоположно вектору скорости и абсолютное значение скорости тела уменьшается. Но работа силы в этом случае, как следует из формулы (1), отрицательна (
совершает положительную работу. Если же вектор силы направлен противоположно вектору перемещения тела, то ускорение тела направлено противоположно вектору скорости и абсолютное значение скорости тела уменьшается. Но работа силы в этом случае, как следует из формулы (1), отрицательна (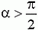 и cos α < 0). Следовательно, отрицательна работа той силы, которая тормозит движение тела, уменьшает его скорость.
и cos α < 0). Следовательно, отрицательна работа той силы, которая тормозит движение тела, уменьшает его скорость.
Произведение 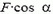 — это величина проекции вектора силы на ось, вдоль которой направлен вектор перемещения тела (рис. 1). Поэтому можно сказать, что работа силы
— это величина проекции вектора силы на ось, вдоль которой направлен вектор перемещения тела (рис. 1). Поэтому можно сказать, что работа силы  равна произведению модуля вектора перемещения тела и проекции вектора силы
равна произведению модуля вектора перемещения тела и проекции вектора силы  на ось, параллельную вектору перемещения.
на ось, параллельную вектору перемещения.
Воспользовавшись этой формулировкой, можно легко доказать следующую теорему.
Теорема 1. Если на тело действует несколько сил, то полная работа, совершенная этими силами, равна сумме работ, совершенных отдельными силами.
Действительно, если на тело действует несколько сил 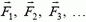 , то эти силы можно всегда заменить их равнодействующей
, то эти силы можно всегда заменить их равнодействующей 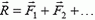 Поэтому общая работа всех сил равна работе равнодействующей:
Поэтому общая работа всех сил равна работе равнодействующей:
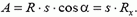
Так как проекция вектора 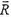 на любую ось равна сумме проекций на эту ось векторов
на любую ось равна сумме проекций на эту ось векторов 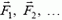 , то
, то
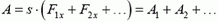
В частности, если на тело действуют две силы, равные по абсолютной величине и направленные в противоположные стороны, то их работа равна нулю. Одна из этих сил совершает некоторую положительную работу, другая — такую же отрицательную.
Нетрудно доказать еще одну теорему.
Теорема 2. Если тело совершает последовательно несколько перемещений: 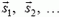 , так что
, так что 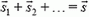 , то работа силы
, то работа силы  равна
равна
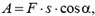
где α — угол между векторами  и
и 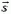 . Заметим, что произведение s·cos α равно проекции вектора перемещения тела на вектор силы (рис. 2) (правильнее сказать — проекции вектора перемещения тела на ось, параллельную вектору силы).
. Заметим, что произведение s·cos α равно проекции вектора перемещения тела на вектор силы (рис. 2) (правильнее сказать — проекции вектора перемещения тела на ось, параллельную вектору силы).
Рис. 2.
Полная работа, совершенная силой  , равна
, равна

Но сумма проекций векторов  на любую ось равна проекции на эту ось вектора
на любую ось равна проекции на эту ось вектора  . Следовательно,
. Следовательно,
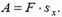
Теперь мы можем сделать вывод: если тело двигалось так, что его полное перемещение равно нулю (тело вернулось в ту же точку, из которой начало двигаться) и во время движения на тело действовала постоянная сила  , то работа силы равна нулю.
, то работа силы равна нулю.
Задача 1. Доказать, что работа постоянной силы не зависит от траектории движения тела.
Как бы ни двигалось тело от точки А к точке В, его перемещение равно вектору 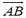 (рис. 3). Следовательно, работа силы
(рис. 3). Следовательно, работа силы  равна
равна 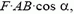 где α — угол между векторами
где α — угол между векторами 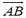 и
и  . Это произведение не зависит от траектории тела.
. Это произведение не зависит от траектории тела.
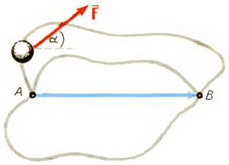
Рис. 3.
До сих пор сила, действующая на тело, была постоянна. Рассмотрим теперь работу переменной силы. В этом случае мы уже не можем воспользоваться формулой (1). Для того чтобы определить работу переменной силы, нужно разбить все движение тела на малые перемещения, такие, чтобы силу на этих перемещениях можно было считать постоянной. На каждом из таких перемещений  работа равна
работа равна
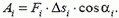
Полная работа равна сумме работ на отдельных перемещениях:
Ясно, что при таком вычислении работы мы получим приближенный результат. Если, скажем, на перемещении 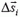 сила меняется на 1 % (вернее, не сила, а произведение
сила меняется на 1 % (вернее, не сила, а произведение 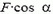 ), то точность наших вычислений тоже будет составлять 1 %. Если нам нужна большая точность, то движение тела следует разбить на еще меньшие перемещения.
), то точность наших вычислений тоже будет составлять 1 %. Если нам нужна большая точность, то движение тела следует разбить на еще меньшие перемещения.
Практически важен случай, когда тело движется прямолинейно, а сила, действующая на тело, меняется по абсолютной величине, в то время как ее направление остается все время одним и тем же. Пусть, например, тело перемещается из одной точки в другую по прямой, а сила  , действующая на тело, направлена всегда вдоль этой прямой, но меняется от точки к точке так, как показано на графике зависимости силы от координаты х (рис. 4).
, действующая на тело, направлена всегда вдоль этой прямой, но меняется от точки к точке так, как показано на графике зависимости силы от координаты х (рис. 4).
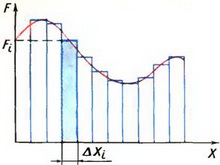
Рис. 4.
Найдем работу этой силы. Разобьем движение тела на маленькие участки Δxi. На каждом из таких участков силу будем считать постоянной и равной некоторому среднему значению Fi. Тогда работа на участке Δxi —
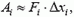
то есть равна площади прямоугольника со сторонами Fi и Δxi. Работа на всем пути, очевидно, равна сумме площадей таких прямоугольников. Так как при уменьшении участков Δxi площадь всех заштрихованных прямоугольников будет стремиться к площади фигуры под графиком силы, то ясно, что работа силы равна в данном случае площади фигуры под графиком зависимости силы от координаты. Если этот график проходит ниже оси X, сила  отрицательна. Это означает, что вектор силы направлен противоположно вектору перемещения тела. Отрицательна и работа этой силы. Значит, при вычислении работы площадь фигуры теперь уже «над графиком силы» нужно взять со знаком минус. Точно так же работу нужно считать отрицательной, если график силы лежит выше оси X, но изменение координаты тела отрицательно.
отрицательна. Это означает, что вектор силы направлен противоположно вектору перемещения тела. Отрицательна и работа этой силы. Значит, при вычислении работы площадь фигуры теперь уже «над графиком силы» нужно взять со знаком минус. Точно так же работу нужно считать отрицательной, если график силы лежит выше оси X, но изменение координаты тела отрицательно.
Итак, мы знаем, как находить работу переменной силы. Найдем таким способом работу силы упругости пружины.
Задача 2. Пружина, находящаяся между телом и упором (рис. 5), сжата на длину Δl. Жесткость пружины k. Тело может без трения двигаться по гладкой плоскости. В начальный момент концы пружины соединены нитью. Затем нить пережигают. Какую работу совершает сила упругости пружины к тому моменту, когда тело проходит положение «равновесия», при котором пружина не деформирована? Какую работу совершает сила упругости к моменту, когда тело оказывается справа от положения равновесия на расстоянии Δli от него.
Рис. 5.
Нарисуем график зависимости силы упругости пружины от положения тела (его координаты х) в системе координат, начало которой совпадает с положением тела в тот момент, когда пружина не деформирована, а направление оси ОХ совпадает с направлением движения тела после пережигания нити (рис. 6).
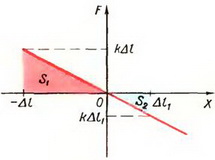
Рис. 6.
Сила упругости пружины пропорциональна деформации пружины:
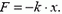
Когда координата тела отрицательна, сила положительна, и наоборот.
Работа A1 совершенная силой упругости пружины к тому моменту, когда тело окажется в положении равновесия, равна площади S1 розового треугольника
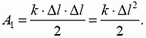
При дальнейшем движении тела направление силы упругости пружины противоположно направлению движения тела; работа отрицательна. Чтобы найти работу силы упругости к моменту, когда координата тела станет равной Δl1 нужно из площади розового треугольника вычесть площадь синего:
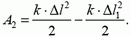
При Δl = Δl1 и A2 = 0.
Рассмотрим теперь другой вопрос — как меняется состояние движущегося тела, если на него действует сила  , совершающая работу А. Будем считать, что тело движется прямолинейно и сила
, совершающая работу А. Будем считать, что тело движется прямолинейно и сила  направлена вдоль линии движения тела. Если перемещение тела равно
направлена вдоль линии движения тела. Если перемещение тела равно 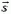 , то
, то
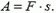
Сила F сообщает телу ускорение 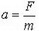 , где m — масса тела. Поэтому
, где m — масса тела. Поэтому
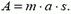
Но как мы знаем из кинематики, 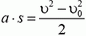 , где υ0— начальная, a υ — конечная скорости тела. Следовательно,
, где υ0— начальная, a υ — конечная скорости тела. Следовательно,
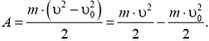
Величина 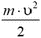 — это кинетическая энергия тела. Следовательно, работа силы
— это кинетическая энергия тела. Следовательно, работа силы  равна изменению кинетической энергии тела.
равна изменению кинетической энергии тела.
Задача 3. На тело, описанное в предыдущей задаче, кроме силы упругости действует еще сила трения тела о плоскость. Масса тела равна m, коэффициент трения тела о плоскость равен f. Каким в этом случае будет максимальное отклонение тела Δl1 от положения, при котором пружина не растянута?
В тот момент, когда координата тела x = Δl1, скорость тела равна нулю, так же как и в начальный момент движения тела. Следовательно, равно нулю и изменение кинетической энергии тела, и работа сил, действующих на тело.
Сила упругости пружины совершает работу
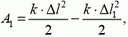
а сила трения — работу
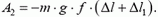
(Работа этой силы отрицательна, так как она направлена против движения тела.) Поэтому:
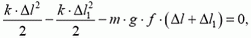
или
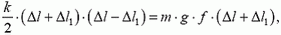
отсюда
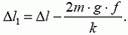
До сих пор, говоря о работе, мы подчеркивали, что это работа силы. Но, как мы знаем, сила действует на данное тело со стороны другого тела. Поэтому вместо того, чтобы говорить о работе силы, можно говорить о работе тела, действующего на движущееся тело с данной силой, или просто о работе тела.
Движущееся тело может совершать работу, например, поднимать другое тело. При этом скорость движущегося тела и его кинетическая энергия будут меняться, причем работа, совершенная движущимся телом, равна изменению его кинетической энергии.
Теперь рассмотрим другой случай. Пусть у нас имеются два тела М1 и М2, которые притягиваются друг к другу, причем тело М2 закреплено неподвижно, а тело М1 движется из точки В (в которой оно было неподвижно) в точку А (рис. 7). (На рисунке показана только сила, действующая на тело М1)
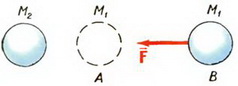
Рис. 7.
Двигаясь под действием силы F, тело М1 может совершить работу
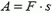
(для простоты мы считаем, что сила F постоянна).
Но тело М1 не обладало запасом кинетической энергии и совершило работу благодаря взаимодействию с телом М2. Поэтому говорят, что тело М1 обладает энергией, которая определяется относительным положением тел М1 и М2. Эту энергию называют потенциальной энергией. Если кинетической энергией обладает тело, то потенциальную энергию уже нельзя отнести к конкретному телу. Потенциальной энергией обладает система тел. Часто, правда, когда перемещение одного из тел и изменение его кинетической энергии мало по сравнению с изменениями движения второго тела, говорят, что потенциальная энергия относится к одному телу — к тому, которое совершает большее перемещение. Например, говорят о потенциальной энергии тела, взаимодействующего с Землей, вместо того чтобы говорить о потенциальной энергии системы тело — Земля.
Потенциальной энергией обладает и может совершить работу любое упруго деформированное тело (система, состоящая из частей упруго деформированного тела), тело, взаимодействующее с Землей (система тело — Земля) и вообще любая система тел, взаимодействующих друг с другом силами упругости или силами тяготения или электрическими кулоновскими силами.
Потенциальная энергия, которой обладает тело, имеет важное отличие от кинетической энергии. Если тело неподвижно (υ = 0), то его кинетическая энергия равна нулю и тело не может совершить работу за cчет изменения его кинетической энергии — ведь кинетическая энергия равна 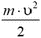 и не может быть отрицательной. Если она равна нулю, то уменьшиться уже не может. В то же время, если тело находится на высоте Н над поверхностью Земли, то, падая, оно может совершить работу, равную работе силы тяжести:
и не может быть отрицательной. Если она равна нулю, то уменьшиться уже не может. В то же время, если тело находится на высоте Н над поверхностью Земли, то, падая, оно может совершить работу, равную работе силы тяжести:
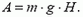
Поэтому можно сказать, что тело обладает потенциальной энергией 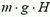 . Но тело может упасть и в шахту глубиной h. Тогда оно сможет совершить работу
. Но тело может упасть и в шахту глубиной h. Тогда оно сможет совершить работу 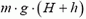 и нам нужно считать, что потенциальная энергия равна
и нам нужно считать, что потенциальная энергия равна 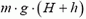 . Так чему же она равна на самом деле?
. Так чему же она равна на самом деле?
Дело в том, что потенциальная энергия определяется, если мы задали положение тел, при котором, как мы считали, потенциальная энергия равна нулю. Это, однако, не означает, что, двигаясь из этого положения, тело не может совершить работу. Просто потенциальная энергия тела будет уменьшаться, становясь отрицательной. Какое из положений тела принять за положение «нулевой потенциальной энергии» — не имеет значения: во все законы и уравнения входит изменение потенциальной энергии, а оно как раз и не зависит от выбора «нуля» потенциальной энергии. Для кинетической энергии «нулем» — «нулевым состоянием» — является состояние, в котором тело неподвижно.
Итак, работа, которую может совершить тело, вначале неподвижное, равна изменению его потенциальной энергии. Если тело М1 взаимодействует только с телом М2, то есть движется только под действием силы  , то его потенциальная энергия уменьшается, то есть уменьшается его возможность совершить работу. Зато в этом случае увеличивается кинетическая энергия тела, причем изменение кинетической энергии равно работе силы
, то его потенциальная энергия уменьшается, то есть уменьшается его возможность совершить работу. Зато в этом случае увеличивается кинетическая энергия тела, причем изменение кинетической энергии равно работе силы  , а изменение потенциальной энергии тоже равно работе силы
, а изменение потенциальной энергии тоже равно работе силы  , но оно отрицательно.
, но оно отрицательно.
Это означает, что изменение потенциальной энергии равно по величине изменению кинетической энергии, так что их сумма остается все время постоянной.
Мы пришли к очень важному выводу — к закону сохранения механической энергии изолированной системы. Изолированной, так как нам было важно, чтобы на тело М1 не действовали другие тела, кроме тела М2, то есть чтобы тела М1 и М2 составляли изолированную систему. Если на данную систему действуют внешние по отношению к ней силы, то полная энергия системы меняется на величину работы этих сил.
Решим теперь несколько задач.
Задача 4. Веревка перекинута через блок, так что концы веревки находятся на одинаковой высоте от земли (рис. 8). Затем блок слегка поворачивают, и веревка начинает соскальзывать с блока под действием силы тяжести. Какую скорость будет иметь веревка в тот момент, когда она полностью слетит с блока? Длина веревки l, масса m.
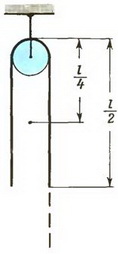
Рис. 8.
В начальный момент центр масс веревки находится на расстоянии 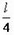 от блока. В тот момент, когда веревка соскользнет с блока, ее центр масс будет находиться на расстоянии
от блока. В тот момент, когда веревка соскользнет с блока, ее центр масс будет находиться на расстоянии 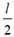 от блока. При этом потенциальная энергия системы веревка — Земля изменится на величину
от блока. При этом потенциальная энергия системы веревка — Земля изменится на величину
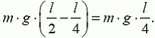
Из закона сохранения энергии следует, что
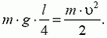
Отсюда
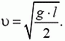
Задача 5. Сила F поднимает груз массы m на высоту Н. Какую работу совершает эта сила? Как меняется потенциальная энергия тела?
Работа силы F равна 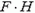 , а изменение потенциальной энергии — величине
, а изменение потенциальной энергии — величине 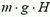 , m — масса тела. Разница
, m — масса тела. Разница 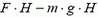 пошла на увеличение кинетической энергии тела.
пошла на увеличение кинетической энергии тела.
Задача 6. Какую мощность должен иметь насос для того, чтобы перекачивать Q литров воды за 1 секунду из колодца, глубина которого h, на поверхность земли? Площадь сечения трубы, через которую перекачивается вода, S.
Вода должна иметь в трубе скорость 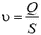 . Это означает, что насос должен за время t совершить работу, равную изменению потенциальной энергии массы воды
. Это означает, что насос должен за время t совершить работу, равную изменению потенциальной энергии массы воды 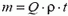 :
:
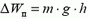
(ρ — плотность воды) и изменению ее кинетической энергии
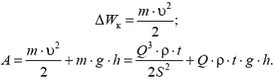
Мощность насоса равна работе, которую он совершает за 1 секунду:
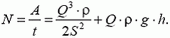
Энергия, так же как и работа, зависит от выбора системы координат. Это естественно — ведь от системы координат зависит как скорость тела, так и его перемещение.
Решим в заключение задачу, в которой выбор системы координат существен.
Задача 7. Два одинаковых по величине и знаку заряда q находятся на расстоянии R друг от друга. На какое минимальное расстояние r могут сблизиться эти заряды, если в начальный момент один из зарядов покоится, а другой движется ему навстречу со скоростью υ?
Часто эту задачу решают, пользуясь системой координат, связанной с зарядом, который вначале покоился. В этой системе координат энергия системы вначале равна сумме ее потенциальной энергии 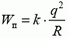 и кинетической энергии движущегося заряда
и кинетической энергии движущегося заряда 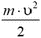
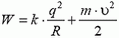
В тот момент, когда заряды находятся на минимальном расстоянии друг от друга, они в этой системе координат неподвижны и энергия системы равна ее потенциальной энергии 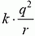 . Из закона сохранения энергии следует, что
. Из закона сохранения энергии следует, что
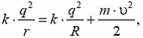
отсюда
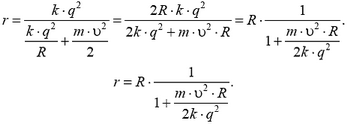
Однако, это решение неверное.
Система координат, связанная с движущимся неравномерно зарядом, неинерциальна. В ней нельзя пользоваться ни II законом Ньютона, ни законом сохранения энергии.
Решим эту задачу, воспользовавшись неподвижной системой координат. Здесь в начальный момент заряды имеют скорости
υ1 = 0 и υ2 = 0,
а энергия системы равна
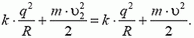
Из закона сохранения импульса следует, что в тот момент, когда расстояние между зарядами минимально, оба заряда движутся с одинаковыми скоростями, равными 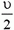 . Энергия системы равна
. Энергия системы равна
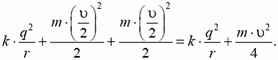
Из закона сохранения энергии найдем:
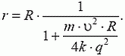
Упражнения
1. Колесо катится без проскальзывания со скоростью υ. Найти кинетическую энергию этого колеса. Масса колеса равна m.
2. Шарик радиуса r = 15 мм и массой m = 5 г погружен в воду на глубину h = 30 см. Когда шарик отпустили, он выпрыгнул из воды на высоту hl = 10 см. Какая часть механической энергии шарика перешла в тепло из-за трения шарика о воду?
3. Найти, воспользовавшись законом сохранения энергии, скорость истечения жидкости из отверстия у дна сосуда, если уровень жидкости находится на высоте h от дна.
| Выложил | alsak |
| Опубликовано | 27.04.09 |
| Просмотров | 15485 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |