Зайцев И.А. Импульс. Закон сохранения импульса // Квант
Зайцев И.А. Импульс. Закон сохранения импульса // Квант. — 1972. — № 3. — С. 58-63.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Эта статья посвящена задачам на одну из самых важных тем школьного курса физики — закон сохранения импульса. Такие задачи можно часто встретить в экзаменационных билетах. В статье использованы задачи, предлагавшиеся на вступительных экзаменах по физике в Московском физико-техническом институте, на физических факультетах Московского государственного университета, Новосибирского государственного университета и в ряде других вузов.
Импульсом (или количеством движения) материальной точки называется произведение ее массы на скорость. Так как скорость — это вектор, а масса — величина скалярная, то импульс — тоже векторная величина. Направление вектора импульса совпадает с направлением вектора скорости.
Если у нас имеется несколько материальных точек или частиц, то можно говорить об импульсе системы материальных точек. Он равен векторной сумме импульсов отдельных точек. Так, например, если у нас имеется две материальные точки, одна из которых имеет массу m1 и скорость 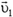 , а вторая — массу m2 и скорость
, а вторая — массу m2 и скорость 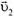 , то импульс
, то импульс 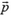 системы этих материальных точек равен сумме
системы этих материальных точек равен сумме 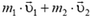 (рис. 1). Важно не забывать, что импульсы частиц складываются векторно, то есть геометрически (по правилу треугольника или по правилу параллелограмма). В том случае, когда скорости частиц направлены вдоль одной прямой, импульсы можно складывать алгебраически. При этом импульсы частиц, движущихся в противоположные стороны, следует брать с противоположными знаками.
(рис. 1). Важно не забывать, что импульсы частиц складываются векторно, то есть геометрически (по правилу треугольника или по правилу параллелограмма). В том случае, когда скорости частиц направлены вдоль одной прямой, импульсы можно складывать алгебраически. При этом импульсы частиц, движущихся в противоположные стороны, следует брать с противоположными знаками.
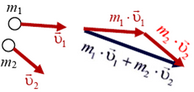
Рис. 1.
Для того чтобы найти импульс тела, различные точки которого имеют разные скорости, его разбивают мысленно на маленькие части (в пределе бесконечно маленькие) и затем складывают импульсы этих частей. Найдем таким способом импульс однородного диска, вращающегося вокруг своей оси. Ясно, что всегда можно найти два таких элемента диска с массами Δm, линейные скорости которых равны по абсолютной величине и противоположно направлены (рис. 2). Сумма импульсов этих элементов, очевидно, равна нулю. А так как диск можно всегда разбить на пары таких элементов, то отсюда следует, что импульс всего диска равен нулю.
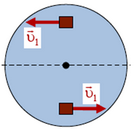
Рис. 2.
Иное дело, если диск катится по горизонтальной поверхности (рис. 3). Пусть скорость центра диска равна 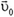 . Скорость любого малого элемента Δm диска можно представить как сумму линейной скорости
. Скорость любого малого элемента Δm диска можно представить как сумму линейной скорости 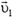 ее вращения вокруг центра диска (в системе координат, связанной с центром диска) и скорости
ее вращения вокруг центра диска (в системе координат, связанной с центром диска) и скорости 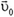 ее поступательного движения:
ее поступательного движения: 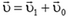 . Импульс диска равен сумме импульсов отдельных его элементов, то есть
. Импульс диска равен сумме импульсов отдельных его элементов, то есть
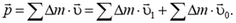
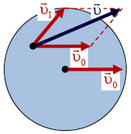
Рис. 3.
Но первый член в этой сумме, очевидно, равен импульсу диска в системе координат, связанной с его центром. В этой системе координат центр диска неподвижен и импульс диска равен нулю. Поэтому импульс диска, катящегося по горизонтальной плоскости, равен 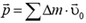 . Вынося постоянный множитель
. Вынося постоянный множитель 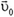 за знак суммы, найдем
за знак суммы, найдем
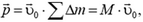
где М — масса диска.
Импульс тела зависит от системы координат. Пусть в системе координат В тело массы m движется со скоростью 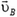 . Его импульс
. Его импульс 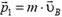 . Система координат В движется со скоростью
. Система координат В движется со скоростью 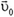 относительно системы координат А. Чтобы найти импульс тела в системе координат A, надо к
относительно системы координат А. Чтобы найти импульс тела в системе координат A, надо к 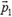 прибавить
прибавить 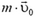 — произведение массы тела на скорость системы координат В относительно системы координат А. Это правило — следствие того, что скорость любой точки в системе координат В складывается из скорости этой точки в системе координат А и скорости системы координат В относительно системы координат А (рис. 4):
— произведение массы тела на скорость системы координат В относительно системы координат А. Это правило — следствие того, что скорость любой точки в системе координат В складывается из скорости этой точки в системе координат А и скорости системы координат В относительно системы координат А (рис. 4): 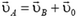 . Отсюда
. Отсюда
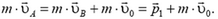
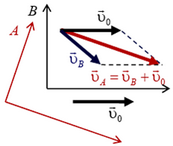
Рис. 4.
Пользуясь понятием «импульс», второй закон Ньютона можно записать так:
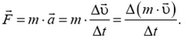
Если на тело действует сила 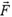 в течение времени Δt то импульс тела изменяется на величину
в течение времени Δt то импульс тела изменяется на величину 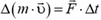 . Произведение силы
. Произведение силы 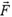 на время ее действия Δt называют импульсом силы. И говорят, что изменение импульса тела равно импульсу действующей на него силы.
на время ее действия Δt называют импульсом силы. И говорят, что изменение импульса тела равно импульсу действующей на него силы.
Воспользовавшись такой формой записи второго закона Ньютона, найдем, например, среднюю силу, действующую на плиту, с которой абсолютно упруго сталкивается шарик массы m, летящий со скоростью 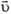 под углом α к плите (рис. 5). Время соударения шарика с плитой равно τ.
под углом α к плите (рис. 5). Время соударения шарика с плитой равно τ.
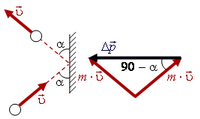
Рис. 5.
Так как столкновение абсолютно упруго, то шарик отскакивает от плиты под таким же углом α, под каким подлетает к ней, и с той же по величине скоростью 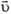 . Нетрудно найти изменение импульса
. Нетрудно найти изменение импульса 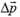 шарика при ударе. Оно равно
шарика при ударе. Оно равно
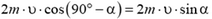
и направлено перпендикулярно плите. Эго означает, что при столкновении шарика с плитой на шарик действует средняя сила
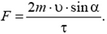
Согласно третьему закону Ньютона точно такая же сила, но направленная противоположно, действует на плиту.
Если одна и та же сила действует на два тела одно и то же время, то импульсы этих тел меняются одинаково, независимо от их начальных масс или скоростей. Пусть, например, две частицы с массами m и 2m движутся так, как показано на рисунке 6, а — первая, частица (m) движется со скоростью 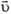 в направлении, перпендикулярном направлению движения второй частицы (2m), скорость которой равна 2
в направлении, перпендикулярном направлению движения второй частицы (2m), скорость которой равна 2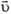 .
.
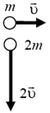
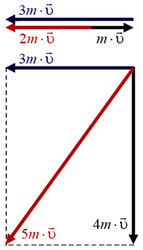
а б
Рис. 6.
На частицы в некоторый момент времени начинают действовать одинаковые силы, причем эти силы действуют на частицы одинаковое время. После прекращения действия сил частица массы m движется со скоростью 2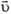 в направлении, противоположном направлению ее первоначального движения. С какой скоростью и в каком направлении движется вторая частица после прекращения действия силы?
в направлении, противоположном направлению ее первоначального движения. С какой скоростью и в каком направлении движется вторая частица после прекращения действия силы?
Найдем импульс силы, действующей на каждую частицу. Нужно не забывать, что импульс и изменение импульса — величины векторные. Импульс первой частицы изменился по направлению и по величине и стал равным 2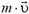 . Изменение импульса первой частицы равно 3
. Изменение импульса первой частицы равно 3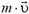 (рис. 6, б). Так как и на вторую частицу действует такая же сила в течение того же самого времени, то и импульс второй частицы меняется на 3
(рис. 6, б). Так как и на вторую частицу действует такая же сила в течение того же самого времени, то и импульс второй частицы меняется на 3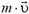 . Сложив первоначальный импульс второй частицы с изменением импульса, найдем, что импульс частицы массы 2m стал равен 5
. Сложив первоначальный импульс второй частицы с изменением импульса, найдем, что импульс частицы массы 2m стал равен 5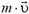 и направлен под углом
и направлен под углом 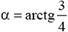 к направлению первоначального движения этой частицы (см. рис. 6, б). Разделив импульс частицы на ее массу, найдем, что скорость частицы массы 2m после прекращения действия силы равна 2,5
к направлению первоначального движения этой частицы (см. рис. 6, б). Разделив импульс частицы на ее массу, найдем, что скорость частицы массы 2m после прекращения действия силы равна 2,5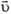 .
.
Теперь решим более сложную задачу.
Космический корабль, имеющий лобовое сечение S = 50 м2 и скорость υ = 10 км/сек, попадает в облако микро-метеоров, плотность которого n = 1 м-3 (то есть в одном кубическом метре пространства находится один микрометеор). Масса каждого микрометеора m = 0,02 г. Насколько должна возрасти сила тяги двигателя, чтобы скорость корабля не изменилась? Удар микрометеоров об обшивку корабля считать абсолютно неупругим.
За время Δt корабль сталкивается с микрометеорами, которые в начальный момент находились от него на расстоянии, меньшем 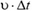 (рис. 7).
(рис. 7).

Рис. 7.
Масса М всех этих микрометеоров равна 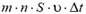 . До столкновения с кораблем скорости и импульсы микрометеоров были равны нулю, а после неупругого столкновения с кораблем скорости микрометеоров стали равны υ. Это означает, что при столкновении микрометеора с обшивкой корабля микрометеор приобретает импульс m·υ. Микрометеоры, попавшие на обшивку корабля за время Δt, приобретают суммарный импульс
. До столкновения с кораблем скорости и импульсы микрометеоров были равны нулю, а после неупругого столкновения с кораблем скорости микрометеоров стали равны υ. Это означает, что при столкновении микрометеора с обшивкой корабля микрометеор приобретает импульс m·υ. Микрометеоры, попавшие на обшивку корабля за время Δt, приобретают суммарный импульс
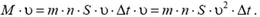
Это означает, что на микрометеоры действует сила
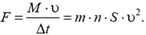
Согласно третьему закону Ньютона такая же по величине сила, но направленная в противоположную сторону, действует на обшивку корабля. Поэтому для того, чтобы при попадании корабля в облако метеоров его скорость не изменилась, сила тяги двигателя корабля должна увеличиться на 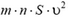 = 105 H.
= 105 H.
Если на тело не действуют силы или действующие силы взаимно уравновешиваются, то импульс тела не меняется. Точно так же, если на систему тел не действуют внешние силы (такая система тел называется замкнутой или изолированной), то суммарный импульс системы тел не меняется.
Решим такую задачу. Нейтрон с энергией E = 10–15 Дж поглощается первоначально неподвижным, ядром кадмия (А = 112). Определить скорость вновь образовавшегося ядра (А = 113).
Система нейтрон — ядро изолированная, и ее импульс не меняется.
Если массу нейтрона обозначить m, а его скорость υ, то 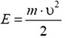 . Отсюда мы найдем, что скорость нейтрона до его столкновения с ядром кадмия была равна
. Отсюда мы найдем, что скорость нейтрона до его столкновения с ядром кадмия была равна 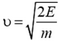 . До столкновения импульс нейтрона был равен
. До столкновения импульс нейтрона был равен 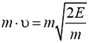 , а импульс ядра был равен нулю. Поэтому до столкновения импульс системы был равен
, а импульс ядра был равен нулю. Поэтому до столкновения импульс системы был равен 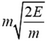 . Если скорость ядра, образовавшегося в результате поглощения нейтрона ядром кадмия, обозначить u, а его массу М, то импульс этого ядра равен М·и. Запишем теперь закон сохранения импульса:
. Если скорость ядра, образовавшегося в результате поглощения нейтрона ядром кадмия, обозначить u, а его массу М, то импульс этого ядра равен М·и. Запишем теперь закон сохранения импульса:
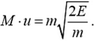
Отсюда найдем, что
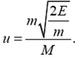
Напомним еще раз, что импульс — величина векторная. Поэтому, когда мы говорим о сохранении импульса изолированной системы, важно помнить, что сохраняется не только величина импульса, но и его направление. Сохраняются и составляющие импульса по любым направлениям, например по двум осям координат.
Решим, используя это, следующую задачу.
Ядро массы m, летящее со скоростью 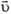 , распадается на две части одинаковой массы, причем один из осколков деления летит со скоростью
, распадается на две части одинаковой массы, причем один из осколков деления летит со скоростью 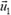 под углом α к направлению полета ядра до его распада. Найти скорость и направление полета второго осколка ядра.
под углом α к направлению полета ядра до его распада. Найти скорость и направление полета второго осколка ядра.
Введем такую систему координат: ось х направим по скорости ядра до распада (рис. 8). Если скорость второго осколка ядра обозначить 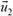 , а угол, который образует вектор
, а угол, который образует вектор 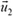 с направлением скорости ядра до распада (с осью х), обозначить β, то на основании закона сохранения импульса мы можем записать:
с направлением скорости ядра до распада (с осью х), обозначить β, то на основании закона сохранения импульса мы можем записать:
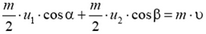
— для составляющих импульсов по оси x,
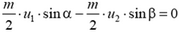
— для составляющих импульсов по оси у.
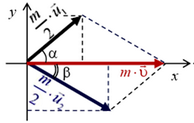
Рис. 8.
Из этих уравнений находим
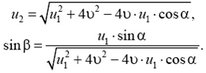
Если система не изолирована и на нее действует некоторая сила 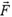 , то полный импульс системы не сохраняется. Однако сохраняется составляющая импульса в направлении, перпендикулярном силе
, то полный импульс системы не сохраняется. Однако сохраняется составляющая импульса в направлении, перпендикулярном силе 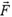 . На этом основано решение большого числа задач.
. На этом основано решение большого числа задач.
Решим, например, такую задачу.
На железнодорожной платформе, движущейся со скоростью υ, укреплено орудие. Ствол орудия направлен в сторону движения платформы и приподнят над горизонтом. Орудие произвело выстрел, после чего скорость платформы уменьшилась в n раз. Найти скорость u снаряда (относительно земли), если он вылетает из ствола под углом α к горизонту. Масса снаряда m, масса платформы с орудием (без снаряда) М.
Система орудие — платформа — снаряд не является изолированной: на нее действует сила тяжести и сила реакции Земли. Однако в горизонтальном направлении на платформу с пушкой и снаряд внешние силы не действуют. Это означает, что горизонтальная составляющая импульса системы не должна при выстреле измениться. Поэтому
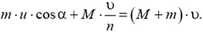
Отсюда
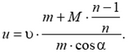
Если система частиц или тел изолирована и ее импульс не меняется, то не меняется и скорость центра масс системы (центра тяжести). В частности, если в некоторый момент система двигалась так, что скорость центра масс была равна нулю, то эта скорость остается равной нулю все время. Поэтому не меняется и положение центра масс.
Рассмотрим пример.
Человек массы m находится на корме лодки массы М, стоящей в пруду. Длина лодки L. На сколько сдвинется лодка относительно берега, если человек перейдет с кормы лодки на нос?
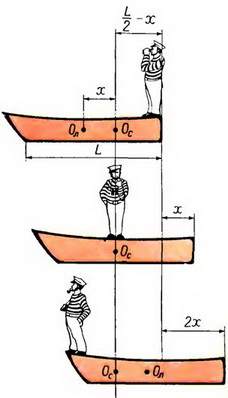
Рис. 9.
Так как в горизонтальном направлении на систему лодка — человек силы не действуют, положение ее центра масс должно сохраниться. Но положение центра масс системы определяется положением центров масс лодки и человека (рис. 9). Пусть первоначально расстояние между центром масс системы (Ос) и центром масс лодки (Ол) равно х.
Тогда 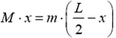 , откуда
, откуда 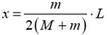 . Когда человек перейдет с кормы лодки на ее середину, то, очевидно, положение его центра масс должно совпадать с положением центра масс системы. Следовательно, и положение центра масс лодки должно также совпадать с положением центра масс системы, то есть лодка должна переместиться на расстояние х. На такое же расстояние переместится лодка при переходе человека на нос. Следовательно, полное перемещение лодки
. Когда человек перейдет с кормы лодки на ее середину, то, очевидно, положение его центра масс должно совпадать с положением центра масс системы. Следовательно, и положение центра масс лодки должно также совпадать с положением центра масс системы, то есть лодка должна переместиться на расстояние х. На такое же расстояние переместится лодка при переходе человека на нос. Следовательно, полное перемещение лодки
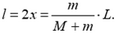
Упражнения
1. Найти среднюю силу, действующую на плиту при абсолютно неупругом столкновении с ней шарика массы m, летящего со скоростью υ в направлении, составляющем с плитой угол α. Время соударения равно τ.
2. С какой силой давит на плечо ручной пулемет при стрельбе, если масса пули m = 10 г, ее скорость при вылете υ = 800 м/сек и скорострельность пулемета n = 600 выстрелов в минуту?
3. Два шарика падают в облаке пыли. Во сколько раз отличаются скорости шариков, если диаметр одного из них вдвое больше диаметра другого?
4. Шарик, летящий горизонтально со скоростью υ, ударяется о тяжелую стальную плиту, движущуюся ему навстречу со скоростью u. С какой скоростью будет двигаться шарик после абсолютно упругого соударения? Силой тяжести пренебречь.
5. Пуля массы m, летящая горизонтально со скоростью υ, попадает в кубик, лежащий на гладком полу, и пробивает его насквозь. Масса кубика М. Скорость пули после вылета равна u. Какая часть первоначальной энергии пули перешла в тепло?
6. При взрыве снаряда массы М = 60 кг образовались три одинаковых осколка. Их общая кинетическая энергия равна E = 2,9 107 Дж. Какую максимальную скорость может иметь один из осколков, если до разрыва снаряд летел со скоростью υ = 800 м/сек?
7. Шарик массы m, летящий со скоростью υ, сталкивается под углом α с кубиком массы М, стоящим на гладком полу (рис. 10). Найти скорость шарика после удара. Удар считать абсолютно упругим.
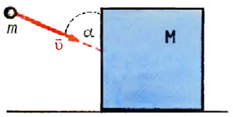
Рис. 10.
8. Шарик массы m, летящий со скоростью υ, составляющей угол α с горизонтом, попадает в покоящуюся платформу с песком массы М (рис. 11) и застревает в песке. Найти скорость платформы.
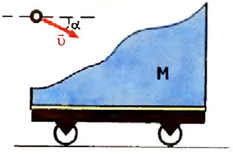
Рис. 11.
Ответы
1. Изменение импульса шарика равно 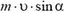 . Поэтому
. Поэтому
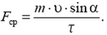
2. 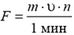 = 80 Н.
= 80 Н.
3. Сила сопротивления, действующая на шарик, пропорциональна площади сечения шарика и квадрату его скорости
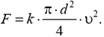
Эта сила растет с увеличением скорости и при некоторой скорости становится равной силе тяжести m·g. После этого скорость шарика не меняется. Так как 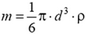 (ρ —плотность шарика), то
(ρ —плотность шарика), то 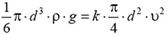 .
.
Отсюда 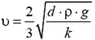 . Таким образом,
. Таким образом, 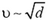 . Это означает, что отношение скоростей шариков равно
. Это означает, что отношение скоростей шариков равно 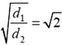 .
.
То есть скорость шарика с вдвое большим диаметром в 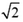 раз больше скорости второго шарика.
раз больше скорости второго шарика.
4. υ + 2u. Указание. Перейти в систему координат, связанную с плитой. Система шарик — плита не изолированная, так как скорость плиты не меняется.
5. Скорость кубика равна 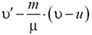 . В тепло перешла энергия
. В тепло перешла энергия 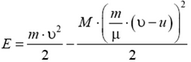 . Разделив это выражение на
. Разделив это выражение на 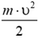 , найдем, что в тепло перейдет
, найдем, что в тепло перейдет 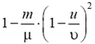 часть энергии пули.
часть энергии пули.
6. υmax ≈ 1500 м/с. Указание. Скорость одного из осколков максимальна, если он будет лететь в направлении полета снаряда, а два других осколка — в противоположную сторону.
7. В вертикальном направлении составляющие скорости шарика 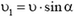 не меняются. В горизонтальном направлении система изолирована. Записав законы сохранения энергии импульса, нетрудно найти, что горизонтальная составляющая скорости шарика будет равна
не меняются. В горизонтальном направлении система изолирована. Записав законы сохранения энергии импульса, нетрудно найти, что горизонтальная составляющая скорости шарика будет равна 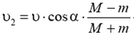 . Скорость шарика после столкновения равна
. Скорость шарика после столкновения равна
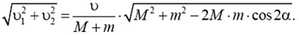
8. 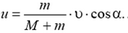
| Выложил | alsak |
| Опубликовано | 18.04.09 |
| Просмотров | 19749 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |