Гольдфарб Н., Новиков В. Импульс тела и системы тел // Квант
Гольдфарб Н., Новиков В. Импульс тела и системы тел // Квант. — 1977. — № 12. — С. 52-58.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Понятие импульса (количества движения) было впервые введено в механику Ньютоном. Напомним, что под импульсом материальной точки (тела) понимается векторная величина 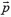 , равная произведению массы тела на его скорость:
, равная произведению массы тела на его скорость:
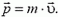
Наряду с понятием импульса тела используется понятие импульса силы. Импульс силы специального обозначения не имеет. В частном случае, когда действующая на тело сила постоянна, импульс силы по определению равен произведению силы на время ее действия: 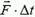 . В общем случае, когда сила изменяется со временем
. В общем случае, когда сила изменяется со временем 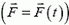 , импульс силы определяется как
, импульс силы определяется как 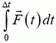 .
.
Используя понятие импульса тела и импульса силы, первый и второй законы Ньютона можно сформулировать следующим образом.
Первый закон Ньютона: существуют системы отсчета, в которых сохраняется неизменным импульс тела, если на него не действуют другие тела или действия других тел компенсируются.
Второй закон Ньютона: в инерциальных системах отсчета изменение импульса тела равно импульсу приложенной к телу силы, то есть
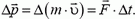
В отличие от привычной галилеевской формы второго закона: 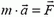 , «импульсная» форма этого закона позволяет применять его к задачам, связанным с движением тел переменной массы (например, ракет) и с движениями в области околосветовых скоростей (когда масса тела зависит от его скорости).
, «импульсная» форма этого закона позволяет применять его к задачам, связанным с движением тел переменной массы (например, ракет) и с движениями в области околосветовых скоростей (когда масса тела зависит от его скорости).
Подчеркнем, что импульс, приобретаемый телом, зависит не только от действующей на тело силы, но и от продолжительности ее действия. Это можно проиллюстрировать, например, на опыте с выдергиванием листа бумаги из-под бутылки — мы оставим ее стоящей практически неподвижно, если сделаем это рывком (рис. 1). Сила трения скольжения, действующая на бутылку в течение очень малого промежутка времени, то есть небольшой импульс силы, вызывает соответственно малое изменение импульса бутылки.

Рис. 1.
Второй закон Ньютона (в «импульсной» форме) дает возможность по изменению импульса тела определить импульс силы, действующей на данное тело, и среднее значение силы за время ее действия. В качестве примера рассмотрим такую задачу.
Задача 1. Мячик массой 50 г ударяет в гладкую вертикальную стенку под углом 30° к ней, имея к моменту удара скорость 20 м/с, и упруго отражается. Определить среднюю силу, действующую на мячик во время удара, если соударение мячика со стенкой длится 0,02 с.
На мячик во время удара действуют две силы — сила 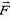 реакции стенки (она перпендикулярна стенке, так как трения нет) и сила тяжести. Пренебрежем импульсом силы тяжести, полагая, что по абсолютной величине он много меньше импульса силы
реакции стенки (она перпендикулярна стенке, так как трения нет) и сила тяжести. Пренебрежем импульсом силы тяжести, полагая, что по абсолютной величине он много меньше импульса силы 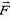 (это предположение мы подтвердим позже). Тогда при столкновении мячика со стенкой проекция его импульса на вертикальную ось Y не изменится, а на горизонтальную ось X — останется такой же по абсолютной величине, но изменит знак на противоположный. В результате, как видно на рисунке 2, импульс мячика изменится на величину
(это предположение мы подтвердим позже). Тогда при столкновении мячика со стенкой проекция его импульса на вертикальную ось Y не изменится, а на горизонтальную ось X — останется такой же по абсолютной величине, но изменит знак на противоположный. В результате, как видно на рисунке 2, импульс мячика изменится на величину 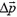 , причем
, причем
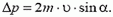
Следовательно, со стороны стенки на мячик действует сила 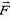 такая, что
такая, что
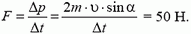
По третьему закону Ньютона мячик действует на стенку с такой же по абсолютной величине силой.
Сравним теперь абсолютные значения импульсов сил 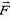 и
и 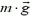 :
:
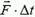 = 1 Н·с,
= 1 Н·с, 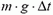 = 0,01 Н·с.
= 0,01 Н·с.
Мы видим, что 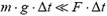 , и импульсом силы тяжести действительно можно пренебречь.
, и импульсом силы тяжести действительно можно пренебречь.
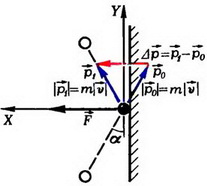
Рис. 2.
Импульс замечателен тем, что под действием одной и той же силы он изменяется одинаково у всех тел, независимо от их массы, если только время действия силы одинаково. Разберем следующую задачу.
Задача 2. Две частицы массами m и 2m движутся во взаимно перпендикулярных направлениях со скоростями соответственно 2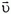 и
и 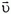 (рис. 3). На частицы начинают действовать одинаковые силы. Определить величину и направление скорости частицы массой 2m в момент времени, когда скорость частицы массой m стала такой, как показано пунктиром: а) на рисунке 3, а; б) на рисунке 3, б.
(рис. 3). На частицы начинают действовать одинаковые силы. Определить величину и направление скорости частицы массой 2m в момент времени, когда скорость частицы массой m стала такой, как показано пунктиром: а) на рисунке 3, а; б) на рисунке 3, б.
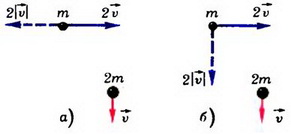
Рис. 3.
Изменение импульсов обеих частиц одно и то же: на них одинаковое время действовали одинаковые силы. В случае а) модуль изменения импульса первой частицы равен
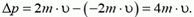
Вектор 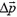 направлен горизонтально (рис. 4, а). Так же меняется и импульс второй частицы. Поэтому модуль импульса второй частицы будет равен
направлен горизонтально (рис. 4, а). Так же меняется и импульс второй частицы. Поэтому модуль импульса второй частицы будет равен
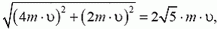
модуль скорости равен 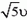 , а угол
, а угол  .
.
Аналогично найдем, что в случае б) модуль изменения импульса первой частицы равен 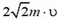 (рис. 4, б). Модуль импульса второй частицы станет равным
(рис. 4, б). Модуль импульса второй частицы станет равным 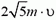 (это нетрудно найти, воспользовавшись теоремой косинусов), модуль скорости этой частицы равен
(это нетрудно найти, воспользовавшись теоремой косинусов), модуль скорости этой частицы равен 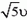 и угол
и угол 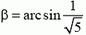 (согласно теореме синусов).
(согласно теореме синусов).
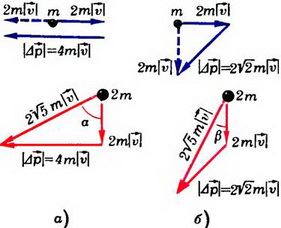
Рис. 4.
Когда мы переходим к системе взаимодействующих тел (частиц), то оказывается, что полный импульс системы — геометрическая сумма импульсов взаимодействующих тел — обладает замечательным свойством сохраняться во времени. Этот закон сохранения импульса является прямым следствием второго и третьего законов Ньютона. В учебнике «Физика 8» этот закон выведен для случая двух взаимодействующих тел, образующих замкнутую систему (эти тела не взаимодействуют ни с какими другими телами). Легко обобщить этот вывод на замкнутую систему, состоящую из произвольного числа n тел. Покажем это.
Согласно второму закону Ньютона изменение импульса i-гo тела системы за малый промежуток времени Δt равно сумме импульсов сил взаимодействия его со всеми другими телами системы:
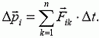
Изменение полного импульса системы 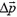 есть сумма изменений импульсов, составляющих систему тел:
есть сумма изменений импульсов, составляющих систему тел: 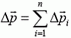 по второму закону Ньютона, равно сумме импульсов всех внутренних сил системы:
по второму закону Ньютона, равно сумме импульсов всех внутренних сил системы:
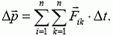
В соответствии с третьим законом Ньютона силы взаимодействия между телами системы попарно одинаковы по абсолютной величине и противоположны по направлению: 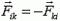 . Поэтому сумма всех внутренних сил равна нулю, значит,
. Поэтому сумма всех внутренних сил равна нулю, значит,
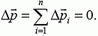
Но если изменение некой величины за произвольный малый промежуток времени Δt равно нулю, то сама эта величина неизменна во времени:
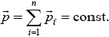
Таким образом, изменение импульса любого из тел, составляющих замкнутую систему, компенсируется противоположным изменением в других частях системы. Иными словами, импульсы тел замкнутой системы могут как угодно изменяться, но сумма их остается постоянной во времени. Если же система не замкнута, то есть на тела системы действуют не только внутренние, но и внешние силы, то, рассуждая подобным образом, придем к выводу, что приращение полного импульса системы за промежуток времени Δt будет равно сумме импульсов внешних сил за тот же промежуток времени:
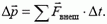
Импульс системы могут изменить только внешние силы.
Если 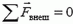 , то незамкнутая система ведет себя подобно замкнутой, и к ней применим закон сохранения импульса.
, то незамкнутая система ведет себя подобно замкнутой, и к ней применим закон сохранения импульса.
Рассмотрим теперь несколько конкретных задач.
Задача 3. Орудие массы m соскальзывает по гладкой наклонной плоскости, составляющей угол α с горизонтом. В момент, когда скорость орудия равна 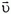 , производят выстрел, в результате которого орудие останавливается, а вылетевший в горизонтальном направлении снаряд «уносит» импульс
, производят выстрел, в результате которого орудие останавливается, а вылетевший в горизонтальном направлении снаряд «уносит» импульс 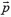 (рис. 5). Продолжительность выстрела равна τ. Каково среднее за время τ значение
(рис. 5). Продолжительность выстрела равна τ. Каково среднее за время τ значение 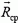 силы реакции со стороны наклонной плоскости?
силы реакции со стороны наклонной плоскости?
Начальный импульс системы тел орудие — снаряд равен 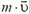 , конечный импульс равен
, конечный импульс равен 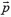 . Рассматриваемая система не замкнута: за время τ она получает приращение импульса
. Рассматриваемая система не замкнута: за время τ она получает приращение импульса 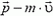 . Изменение импульса системы обусловлено действием двух внешних сил: силы реакции
. Изменение импульса системы обусловлено действием двух внешних сил: силы реакции 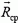 (перпендикулярной наклонной плоскости) и силы тяжести
(перпендикулярной наклонной плоскости) и силы тяжести 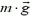 , поэтому можно записать
, поэтому можно записать
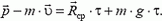
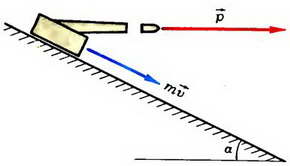
Рис. 5.
Представим это соотношение графически (рис. 6). Из рисунка сразу видно, что искомое значение 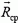 определяется формулой
определяется формулой
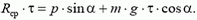
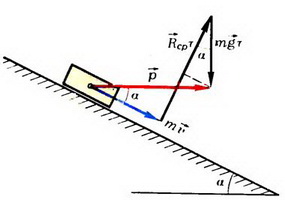
Рис. 6.
Импульс — величина векторная, поэтому закон сохранения импульса можно применять к каждой из его проекций на оси координат. Иначе говоря, если сохраняется 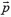 , то независимо сохраняются px, py и pz (если задача трехмерная).
, то независимо сохраняются px, py и pz (если задача трехмерная).
В случае, когда сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление — нуль, проекция полного импульса на это же направление сохраняется неизменной. Например, при движении системы в поле силы тяжести сохраняется проекция ее импульса на любое горизонтальное направление.
З
адача 4. Горизонтально летящая пуля попадает в деревянный брусок, подвешенный на очень длинном шнуре, и застревает в бруске, сообщив ему скорость u = 0,5 м/с. Определить скорость пули перед ударом. Масса пули m = 15 г, масса бруска М = 6 кг.
Торможение пули в бруске — сложный процесс, но для решения задачи нет никакой необходимости вникать в его детали. Так как в направлении скорости пули до удара и скорости бруска после застревания пули (подвес очень длинный, поэтому скорость бруска горизонтальна) не действуют внешние силы, то можно применить закон сохранения импульса:
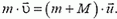
Отсюда скорость пули
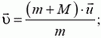 υ » 200 м/с.
υ » 200 м/с.
В реальных условиях — в условиях земного притяжения — не существует замкнутых систем, если не включать в них Землю. Однако, если взаимодействие между телами системы много сильнее, чем их взаимодействие с Землей, то можно с большой точностью применять закон сохранения импульса. Так можно поступать, например, при всех кратковременных процессах: взрывах, столкновениях и т. п. (см. например, задачу 1).
Задача 5. Третья ступень ракеты состоит из ракеты-носителя массой mp = 500 кг и головного конуса массой mк = 10 кг. Между ними помещена сжатая пружина. При испытаниях на Земле пружина сообщила конусу скорость υ = 5,1 м/с по отношению к ракете-носителю. Каковы будут скорости конуса υк и ракеты-носителя υp, если их отделение произойдет на орбите при движении со скоростью υ = 8000 м/с?
Согласно закону сохранения импульса
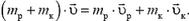
Кроме того,
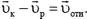
Из этих двух соотношений получим
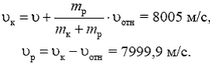
Эту задачу можно решать и в системе отсчета, движущейся со скоростью 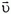 в направлении полета. Заметим в связи с этим, что если импульс сохраняется в одной инерциальной системе отсчета, то он сохраняется и в любой другой инерциальной системе отсчета.
в направлении полета. Заметим в связи с этим, что если импульс сохраняется в одной инерциальной системе отсчета, то он сохраняется и в любой другой инерциальной системе отсчета.
Закон сохранения импульса лежит в основе реактивного движения. Струя газа, вырывающаяся из ракеты, уносит импульс. Этот импульс должен быть скомпенсирован таким же по модулю изменением импульса оставшейся части системы ракета-газ.
Задача 6. Из ракеты массой М выбрасываются продукты сгорания порциями одной и той же массы m со скоростью 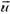 относительно ракеты. Пренебрегая действием силы тяжести, определить скорость ракеты, которой она достигнет после вылета n-й порции.
относительно ракеты. Пренебрегая действием силы тяжести, определить скорость ракеты, которой она достигнет после вылета n-й порции.
Пусть 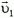 — скорость ракеты относительно Земли после выброса 1-й порции газа. По закону сохранения импульса
— скорость ракеты относительно Земли после выброса 1-й порции газа. По закону сохранения импульса
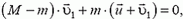
где 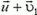 — скорость первой порции газа относительно Земли в момент разделения системы ракета-газ, когда ракета уже приобрела скорость
— скорость первой порции газа относительно Земли в момент разделения системы ракета-газ, когда ракета уже приобрела скорость 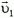 . Отсюда
. Отсюда
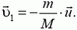
Найдем теперь скорость 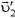 ракеты после вылета второй порции. В системе отсчета, движущейся со скоростью
ракеты после вылета второй порции. В системе отсчета, движущейся со скоростью 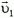 ракета перед вылетом второй порции неподвижна, а после выброса приобретает скорость
ракета перед вылетом второй порции неподвижна, а после выброса приобретает скорость 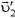 . Воспользовавшись предыдущей формулой и сделав в ней замену
. Воспользовавшись предыдущей формулой и сделав в ней замену 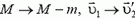 , получим
, получим
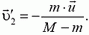
Тогда 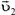 будет равно
будет равно
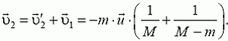
Продолжая этот процесс дальше, нетрудно получить
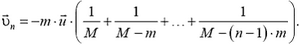
Закону сохранения импульса можно придать другую форму, упрощающую решение многих задач, если ввести понятие центра масс (центра инерции) системы. Координаты центра масс (точки с) по определению связаны с массами и координатами частиц, составляющих систему, следующими соотношениями:
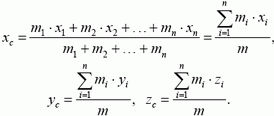
Следует заметить, что центр масс системы в однородном поле тяжести совпадает с центром тяжести.
Для выяснения физического смысла центра масс вычислим его скорость 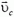 , а точнее, проекции этой скорости. По определению
, а точнее, проекции этой скорости. По определению
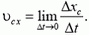
В этой формуле
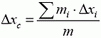 и
и 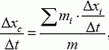
поэтому
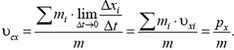
Точно так же найдем, что
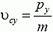 и
и 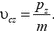
Отсюда следует, что
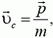 или
или 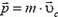
— полный импульс системы равен произведению массы системы на скорость ее центра масс.
Центр масс (центр инерции) системы, таким образом, приобретает смысл точки, скорость которой равна скорости движения системы как целого. Если 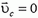 , то система как целое покоится, хотя при этом тела системы относительно центра инерции могут двигаться произвольным образом.
, то система как целое покоится, хотя при этом тела системы относительно центра инерции могут двигаться произвольным образом.
С помощью формулы 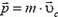 закон сохранения импульса может быть сформулирован так: центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным. Если система не замкнута, то можно показать, что
закон сохранения импульса может быть сформулирован так: центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным. Если система не замкнута, то можно показать, что
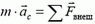
— ускорение центра инерции определяется равнодействующей всех внешних сил, приложенных к системе.
Рассмотрим такие задачи.
3адача 7. На концах однородной платформы длиной l находятся два человека, массы которых 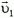 и
и 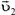 (рис. 7). Первый прошел до середины платформы. На какое расстояние х надо переместиться по платформе второму человеку, чтобы тележка вернулась на прежнее место? Найти условие, при котором задача имеет решение.
(рис. 7). Первый прошел до середины платформы. На какое расстояние х надо переместиться по платформе второму человеку, чтобы тележка вернулась на прежнее место? Найти условие, при котором задача имеет решение.
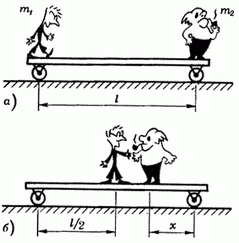
Рис. 7.
Найдем координаты центра масс системы в начальный и конечный моменты и приравняем их (поскольку центр масс остался на том же месте). Примем за начало координат точку, где в начальный момент находился человек массой m1. Тогда

(здесь М — масса платформы). Отсюда
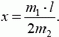
Очевидно, что если m1 > 2m2, то x > l — задача теряет смысл.
Задача 8. На нити, перекинутой через невесомый блок, подвешены два груза, массы которых m1 и m2 (рис. 8). Найти ускорение центра масс этой системы, если m1 > m2.
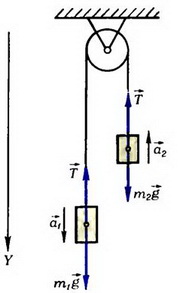
Рис. 8.
Система, состоящая из грузов, нити и блока, незамкнутая. Извне на систему действуют силы тяжести грузов 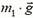 и
и 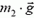 и сила, приложенная к блоку со стороны подвеса, равная удвоенной силе натяжения нити
и сила, приложенная к блоку со стороны подвеса, равная удвоенной силе натяжения нити 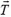 (см. рис. 8). Напишем уравнение движения системы в проекциях на вертикальную ось Y, направленную вниз:
(см. рис. 8). Напишем уравнение движения системы в проекциях на вертикальную ось Y, направленную вниз:
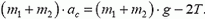
Силу 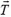 можно найти, написав уравнения движения для каждого груза в отдельности (учтем при этом, что a1 = –a2 = a):
можно найти, написав уравнения движения для каждого груза в отдельности (учтем при этом, что a1 = –a2 = a):
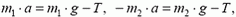
откуда
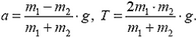
Подставив полученное значение 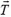 в наше исходное уравнение, найдем, что
в наше исходное уравнение, найдем, что
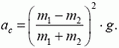
Задачу можно решить и по-другому. Непосредственно из определения центра масс следует, что
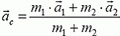
(здесь 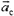 — ускорение центра масс,
— ускорение центра масс, 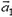 и
и 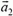 — ускорения грузов m1 и m2 соответственно), или в проекциях на ось Y:
— ускорения грузов m1 и m2 соответственно), или в проекциях на ось Y:
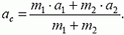
Учитывая, что
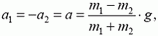
получим
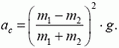
Упражнения
1. Два человека стоят на коньках на расстоянии l друг от друга. Один из них бросает мяч массы m, другой подхватывает его через промежуток времени t. С какой скоростью начнет скользить человек, бросавший мяч, если его масса М?
2. По клину с углом при основании α, который может двигаться по гладкому горизонтальному столу, движется заводной игрушечный автомобиль с постоянной по отношению к клину скоростью 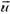 . Как велика скорость клина и чему равна сила давления автомобиля на клин? Масса клина М, автомобиля m. Автомобиль начал двигаться, когда клин покоился.
. Как велика скорость клина и чему равна сила давления автомобиля на клин? Масса клина М, автомобиля m. Автомобиль начал двигаться, когда клин покоился.
3. Гимнаст массой М, имея при себе груз массой m, прыгает под углом α к горизонту с начальной скоростью 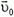 . В момент, когда им достигнута наибольшая высота, он бросает груз назад с горизонтальной скоростью
. В момент, когда им достигнута наибольшая высота, он бросает груз назад с горизонтальной скоростью 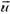 относительно себя. На сколько увеличилась дальность прыжка от бросания груза?
относительно себя. На сколько увеличилась дальность прыжка от бросания груза?
4. Снаряд выброшен орудием с начальной скоростью 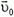 под углом α к горизонту. В верхней точке своей параболической траектории снаряд разрывается на два осколка с массами m1 и m2. Осколок массой m1 после взрыва падает вертикально, имея начальную скорость
под углом α к горизонту. В верхней точке своей параболической траектории снаряд разрывается на два осколка с массами m1 и m2. Осколок массой m1 после взрыва падает вертикально, имея начальную скорость 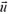 . Найти уравнение движения второго осколка.
. Найти уравнение движения второго осколка.
5. Лодка массой М неподвижно стоит в озере. На корме и на носу лодки на расстоянии l друг от друга находятся рыболовы массами m1 и m2 (m1 > m2). Рыболовы меняются местами. На сколько переместится при этом лодка? Сопротивлением воды пренебречь.
6. На краю покоящегося плота массой М стоят n мальчиков, масса каждого из которых равна m. Найти скорость плота после того, как мальчики спрыгнут с одной и той же горизонтальной скоростью и относительно плота: а) одновременно; б) поочередно. В каком случае скорость плота будет больше? Сопротивлением воды пренебречь.
7. На тележке стоят два бака, соединенных между собой трубкой с краном. Один из них наполнен водой (рис. 9). При открывании крана вода переливается в другой бак. Описать характер движения тележки.
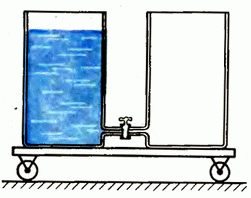
Рис. 9.
Ответы
1. 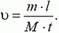
2. 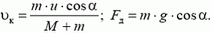
3. 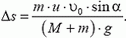 Указание. Удобнее всего решать задачу в системе отсчета, движущейся поступательно со скоростью
Указание. Удобнее всего решать задачу в системе отсчета, движущейся поступательно со скоростью 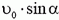 .
.
4. 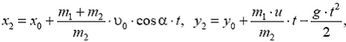 где
где 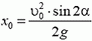 и
и 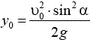 (начало координат находится в точке, в которой установлено орудие).
(начало координат находится в точке, в которой установлено орудие).
5. 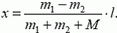
6. а) 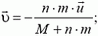 б)
б) 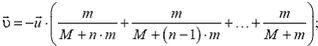 скорость плота больше в случае б).
скорость плота больше в случае б).
7. Положение центра масс системы не может измениться под действием внутренних сил. Поэтому вначале тележка должна двигаться в сторону, противоположную движению воды. После того, как уровни в баках окончательно сравняются, движение тележки прекратится.
| Выложил | alsak |
| Опубликовано | 12.04.09 |
| Просмотров | 27014 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |