Овчинников А., Плис В. Теорема об изменении кинетической энергии в задачах механики // Квант
Овчинников А., Плис В. Теорема об изменении кинетической энергии в задачах механики // Квант. — 1998. — № 1. — С. 47-49.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Эта теорема утверждает, что изменение (приращение) кинетической энергии материальной точки равно работе всех сил, приложенных к этой точке:
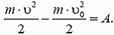
Здесь m — масса материальной точки, υ и υ0 — величины ее конечной и начальной скоростей, A — работа всех сил.
Рассмотрим несколько конкретных задач.
Задача 1. Чтобы затащить на горку санки массой m = 5 кг, прикладывая постоянную силу вдоль наклонной плоской поверхности горки, необходимо совершить работу не менее A = 480 Дж. С какой скоростью достигнет основания горки девочка на этих санках, если она съедет с горки с нулевой начальной скоростью по кратчайшему пути? Угол наклона плоскости горки к горизонту α = arctg 0,2. Коэффициент трения скольжения между санками и горкой μ = 0,1.
На санки, движущиеся по горке вверх, действуют четыре силы: сила тяжести 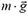 , сила нормальной реакции
, сила нормальной реакции  , сила трения
, сила трения  , и сила тяги
, и сила тяги 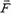 . В соответствии со вторым законом Ньютона, записанным в проекциях на перпендикуляр к наклонной плоскости горки, находим N1 = m·g·cos α. Тогда для величины силы трения скольжения имеем
. В соответствии со вторым законом Ньютона, записанным в проекциях на перпендикуляр к наклонной плоскости горки, находим N1 = m·g·cos α. Тогда для величины силы трения скольжения имеем
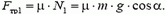
По теореме об изменении кинетической энергии для санок, очень медленно движущихся вверх, получим
0 – 0 = A + Aтяж1 + Aтр1.
В левой части равенства стоит разность кинетических энергий санок в конце и в начале движения, а в правой части записаны следующие величины: A — работа силы тяги,
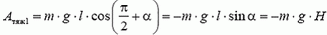
— работа силы тяжести (здесь l — длина горки, H — ее высота),
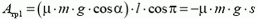
— работа силы трения (здесь s — длина основания горки). Работа силы реакции, перпендикулярной перемещению, равна нулю. Таким образом, описание подъема санок приводит к равенству
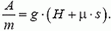
На спускающиеся с горки санки с девочкой действуют три силы: сила тяжести 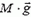 (M — сумма масс девочки и санок), сила нормальной реакции величиной M·g·cos α и сила трения, равная μ·M·g·cos α. По теореме об изменении кинетической энергии теперь имеем
(M — сумма масс девочки и санок), сила нормальной реакции величиной M·g·cos α и сила трения, равная μ·M·g·cos α. По теореме об изменении кинетической энергии теперь имеем
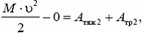
где в левой части равенства стоит разность кинетических энергий девочки с санками у основания горки и на старте (в верхней части горки), в правой части — сумма работ всех сил:
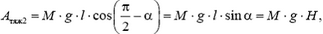
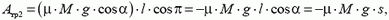
а работа силы реакции, как и на этапе подъема равна нулю. После простых преобразований находим
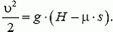
Наконец, деление этой формулы на полученную ранее аналогичную формулу приводит окончательно к ответу на вопрос задачи:
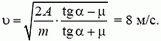
Задача 2. В водоеме укреплена вертикальная труба с гладкой внутренней поверхностью, вдоль которой герметично может скользить легкий поршень. Нижний конец трубы погружен в воду (рис. 1). Поршень, лежавший вначале на поверхности воды, медленно поднимают на высоту H = 15 м. Найдите работу, которую необходимо при этом совершить. Площадь поршня S = 1 дм2, атмосферное давление p0 = 105 Па, плотность воды ρ = 103 кг/м3, ускорение свободного падения g = 10 м/с2. Давлением насыщенных паров воды пренебречь.
Рис. 1
Если поднять поршень на небольшую высоту h, приложив к нему направленную вертикально вверх силу величиной F, давление поршня на воду уменьшится. Таким образом, на одной и той же горизонтальной плоскости давление в воде под поршнем будет меньше, чем под открытой поверхностью в водоеме. Под действием этой разности давлений вода втягивается в трубу и поднимается на высоту h, в результате чего давление у основания водяного столба, равное сумме давления поршня на воду 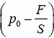 и гидростатического давления ρ·g·h, станет равным атмосферному p0:
и гидростатического давления ρ·g·h, станет равным атмосферному p0:
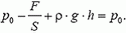
Отсюда находим
F = ρ·g·h·S.
Заметим, что при высоте подъема воды 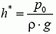 = 10 м давление поршня на воду станет равным нулю, гидростатическое давление станет равным атмосферному давлению и поршень оторвется от воды. Между водой и нижней поверхностью поршня возникнет увеличивающееся пустое пространство (считается, что водяного пара или другого газа в этом пространстве нет). Минимальная сила, которую следует прикладывать к поршню при дальнейшем его подъеме, постоянна и равна p0·S.
= 10 м давление поршня на воду станет равным нулю, гидростатическое давление станет равным атмосферному давлению и поршень оторвется от воды. Между водой и нижней поверхностью поршня возникнет увеличивающееся пустое пространство (считается, что водяного пара или другого газа в этом пространстве нет). Минимальная сила, которую следует прикладывать к поршню при дальнейшем его подъеме, постоянна и равна p0·S.
Зависимость величины F от h представлена в виде графика на рисунке 2.
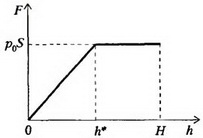
Рис. 2
Площадь под графиком и равна искомой работе:
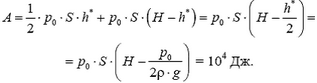
Задача 3. Лыжник съезжает с нулевой начальной скоростью, не отталкиваясь палками, со склона холма по прямой, составляющей некоторый угол с горизонтальной плоскостью, и, проехав по склону расстояние s0 = 60 м, останавливается, увязнув в снегу. Условия движения таковы, что сила сопротивления, действующая на лыжника со стороны снега, пропорциональна пройденному пути; коэффициент пропорциональности k = 6,4 Н/м. Найдите величину максимальной скорости лыжника при спуске, если его масса с инвентарем m = 90 кг. Сопротивлением воздуха пренебречь.
На съезжающего по склону холма лыжника действуют три силы: сила тяжести 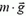 , сила реакции, перпендикулярная траектории, и сила сопротивления, равная Fc = k·s, где s — длина пройденного пути, и направленная по касательной к траектории лыжника противоположно вектору его скорости.
, сила реакции, перпендикулярная траектории, и сила сопротивления, равная Fc = k·s, где s — длина пройденного пути, и направленная по касательной к траектории лыжника противоположно вектору его скорости.
По теореме об изменении кинетической энергии, для отрезка пути s ≤ s0 имеем
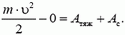
Здесь υ — величина скорости лыжника в момент, когда он прошел путь s. Работа постоянной силы тяжести находится по формуле

где α — угол наклона прямолинейной траектории лыжника к горизонту. Работа силы сопротивления, во-первых, отрицательна (так как сила и перемещение противонаправлены), а во-вторых, — это работа переменной силы. График зависимости Fc от s представляет собой прямую линию, проходящую через начало координат. Как и в задаче 1, площадь под графиком имеет смысл величины соответствующей работы:
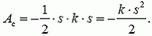
Возвращаясь к теореме об изменении кинетической энергии, получаем
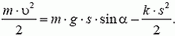
Искомая в задаче максимальная скорость соответствует максимальному значению правой части этого равенства. Поскольку правая часть равенства — квадратичная функция пути, ее максимальное значение находится при значении s, равном полусумме путей s1 и s2, обращающих ее в ноль. Ясно, что s1 = 0 и 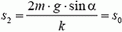 . Таким образом, при
. Таким образом, при 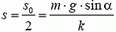 кинетическая энергия лыжника максимальна:
кинетическая энергия лыжника максимальна:
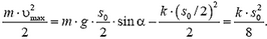
Отсюда находим искомую скорость:
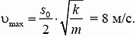
При расчете работы силы сопротивления принят во внимание линейный рост силы сопротивления с увеличением смещения s. Более того, суммарная сила (m·g·sin α – k·s) имеет характер квазиупругой возвращающей силы с положением равновесия при s = s0/2. Следовательно, от старта до остановки лыжник движется по гармоническому закону, достигая максимальной скорости в положении s = s0/2, причем s0/2 — максимальное смещение от положения равновесия (амплитуда колебаний). Из кинематики гармонических колебаний известна связь амплитуд скорости и смещения:
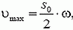
где 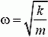 — циклическая частота колебаний. Таким образом, результат для υmax можно получить и в терминах амплитуд колеблющихся величин.
— циклическая частота колебаний. Таким образом, результат для υmax можно получить и в терминах амплитуд колеблющихся величин.
***
Особый интерес представляет теорема об изменении кинетической энергии для системы нескольких взаимодействующих тел, движущихся относительно друг друга. Рассмотрим случай двух взаимодействующих тел.
Пусть 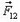 — сила, действующая на тело 1 массой m1 со стороны тела 2 массой m2, a
— сила, действующая на тело 1 массой m1 со стороны тела 2 массой m2, a 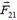 — сила, действующая на тело 2 со стороны тела 1. В соответствии с третьим законом Ньютона,
— сила, действующая на тело 2 со стороны тела 1. В соответствии с третьим законом Ньютона,
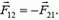
Пусть также 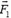 — сумма всех сил, действующих на тело 1 со стороны всех тел, кроме тела 2, т.е. это есть сумма всех внешних сил, приложенных к телу 1. Аналогичный смысл имеет сила
— сумма всех сил, действующих на тело 1 со стороны всех тел, кроме тела 2, т.е. это есть сумма всех внешних сил, приложенных к телу 1. Аналогичный смысл имеет сила 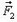 в отношении тела 2. Для каждого из двух тел запишем теорему об элементарном приращении его кинетической энергии:
в отношении тела 2. Для каждого из двух тел запишем теорему об элементарном приращении его кинетической энергии:
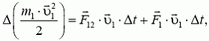
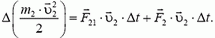
Складывая почленно эти равенства, с учетом третьего закона Ньютона, находим
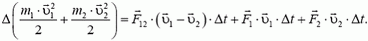
В левой части этого равенства записано элементарное приращение кинетической энергии системы двух тел. Первое слагаемое в правой части — это вычисленная в системе отсчета, связанной с телом 2, элементарная работа силы, действующей на тело 1 со стороны тела 2. Второе и третье слагаемые — это элементарные работы внешних сил.
Теперь — задача.
Задача 4. На гладкой горизонтальной плоскости покоится доска массой m1. На доску со скоростью 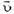 въезжает шайба массой m2 (рис. 3). Какой должна быть минимальная длина доски l, чтобы шайба не соскользнула с нее? Коэффициент трения скольжения между шайбой и доской μ, размер шайбы мал по сравнению с длиной доски.
въезжает шайба массой m2 (рис. 3). Какой должна быть минимальная длина доски l, чтобы шайба не соскользнула с нее? Коэффициент трения скольжения между шайбой и доской μ, размер шайбы мал по сравнению с длиной доски.
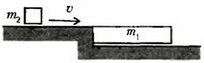
Рис. 3
Запишем теорему об изменении кинетической энергии системы тел m1 и m2:
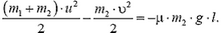
Величину u конечной скорости шайбы и доски можно найти из закона сохранения импульса
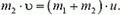
Решая эти два уравнения, находим окончательно
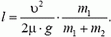
Конечно, можно было бы решить задачу, опираясь на теорему об изменении кинетической энергии для каждого тела. В таком случае соответствующая система уравнений имеет вид
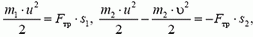
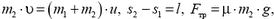
где s1 и s2 — величины перемещений тел 1 и 2 соответственно относительно неподвижной системы отсчета. Решая эту систему уравнений, приходим к тому же ответу на вопрос задачи, что и в первом варианте ее решения.
***
В заключение рассмотрим задачу, в которой теорема об изменении кинетической энергии используется наоборот: по известному приращению кинетической энергии находится работа.
Задача 5. Найдите коэффициент полезного действия водометного двигателя реактивного катера, движущегося с постоянной скоростью. Площадь входного отверстия двигателя S1, выходного S2.
Выберем систему отсчета, связанную с катером. Пусть через двигатель ежесекундно проходит масса μ воды, причем попадает она в двигатель со скоростью υ1 (это скорость движения катера), а выходит со скоростью υ2. Импульс этой массы воды за секунду увеличивается на 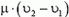 , следовательно, сила тяги двигателя равна
, следовательно, сила тяги двигателя равна 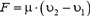 , a его полезная мощность —
, a его полезная мощность — 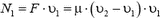 . Полная мощность двигателя равна приращению кинетической энергии воды, прошедшей через двигатель в единицу времени:
. Полная мощность двигателя равна приращению кинетической энергии воды, прошедшей через двигатель в единицу времени:
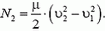
Коэффициент полезного действия η двигателя равен отношению полезной мощности к полной:
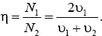
Из условия неразрывности струи воды и несжимаемости воды 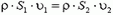 следует, что
следует, что
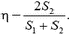
Заметим, что при решении задачи в системе отсчета, связанной с берегом, полезная мощность двигателя по-прежнему будет равна 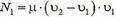 . Полная же мощность
. Полная же мощность 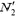 будет расходоваться на преодоление силы сопротивления, которая по величине равна силе тяги, и на ежесекундное увеличение кинетической энергии воды, скорость которой при прохождении через двигатель увеличивается от 0 до υ2 – υ1, т.е.
будет расходоваться на преодоление силы сопротивления, которая по величине равна силе тяги, и на ежесекундное увеличение кинетической энергии воды, скорость которой при прохождении через двигатель увеличивается от 0 до υ2 – υ1, т.е.
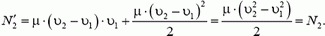
Таким образом, величина коэффициента полезного действия водометного двигателя в обеих системах отсчета определяется одним и тем же соотношением.
Упражнения
1. Когда тело двигалось вниз по наклонной плоскости, на высоте H от ее основания оно имело скорость υ1, а когда оно двигалось вверх после упругого удара о стенку у основания плоскости, его скорость на той же высоте H была равна υ2 (рис. 4). Определите скорость тела при ударе о стенку.
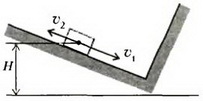
Рис. 4
2. Однородный брусок, скользящий по гладкой горизонтальной поверхности, попадает на шероховатый участок этой поверхности шириной l, коэффициент трения о который μ. При какой минимальной начальной скорости брусок преодолеет шероховатый участок поверхности?
3. Кабина лифта массой m = 3·103 кг опускается с постоянной скоростью υ = 10 м/с. Внезапно происходит полная остановка барабана, с которого сматывается трос. Найдите максимальное удлинение троса, если коэффициент упругости для той его длины, при которой произошла остановка барабана, равен k = 106 Н/м.
4. По гладкой горизонтальной плоскости стола равномерно со скоростью υ скользит доска массой m1 вместе с расположенной на ней небольшой шайбой массой m2 (рис. 5). После абсолютно упругого столкновения доски с вертикальной неподвижной стеной шайба перемещается по доске на l. Определите коэффициент трения скольжения между шайбой и доской.
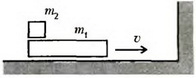
Рис. 5
5. Оцените мощность двигателя, необходимую для поддержания в воздухе вертолета массой M = 500 кг с лопастями длиной l = 3 м. Считайте, что весь воздух под вращающимися лопастями движется однородным потоком вниз. Давление и температура воздуха равны, соответственно, p = 105 Па и T = 300 К, молярная масса воздуха M = 29 г/моль, универсальная газовая постоянная R = 8,31 Дж/(моль·К).
Ответы
1. 
2. 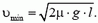
3. 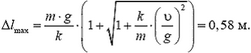
4. 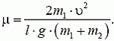
5. 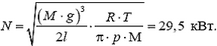
| Выложил | alsak |
| Опубликовано | 28.03.09 |
| Просмотров | 28234 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |