Афонин А. и др. Что покажет динамометр? // Квант
Афонин А., Капшай В., Капшай М., Шолох В. Что покажет динамометр? //Квант. — 1992. — № 2. — С. 47-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Задачи о показаниях измерительных приборов часто кажутся простыми. Дело, вероятно, в том, что, когда вводится новая физическая величина, всегда сразу же дается рецепт, с помощью какого устройства и как именно следует эту величину измерять. В дальнейшем, считая вопрос исчерпанным, к тонкостям процесса измерения возвращаются редко.
Это относится и к измерениям с помощью простейших приборов, например — пружинного динамометра.
Хорошо известно, что если к обоим концам динамометра приложены одинаковые по модулю силы F0, то динамометр покажет именно это значение силы. При этом пружина динамометра растянется, и ее абсолютное удлинение Δl0 определится соотношением 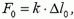 где k — жесткость пружины. Вроде бы все просто. Но…
где k — жесткость пружины. Вроде бы все просто. Но…
Задача 1. 3а один конец пружинного динамометра тянут с силой F1 = 50 H, за другой — с силой F2 = 70 H. Что покажет динамометр?
На вопрос этой задачи отвечают обычно, что динамометр покажет либо F2, либо F1. Встречаются также ответы F2 + F1 и F2 – F1. На самом деле ни один из этих ответов не является верным. А что же верно? Об этом — чуть позже.
С помощью пружинного динамометра можно также определить массу m тела, поскольку нетрудно измерить силу тяжести, равную m·g. Вроде бы тоже все просто. Однако...
Задача 2. Как определить массу пружины динамометра, имея в своем распоряжении только этот динамометр?
Оказывается, обе сформулированные задачи тесно связаны друг с другом, хотя на первый взгляд это может показаться и странным. Скоро вы в этом убедитесь. Но прежде рассмотрим еще одну, несколько более простую задачу и решим ее.
Задача 3. За один конец динамометра тянут с силой, равной F. Что покажет динамометр?
Для начала попытаемся четко понять, что означает этот вопрос.
Ясно, что, глядя на динамометр, мы можем сказать только, растянулась его пружина или нет и если растянулась, то насколько. Мы можем также измерить величину абсолютного удлинения пружины в единицах длины, например в сантиметрах. Определить же значение силы можно лишь после предварительной градуировки шкалы динамометра в единицах силы, например в ньютонах, с помощью закона Гука.
Очень важными являются также следующие два условия: 1) во время измерения динамометр покоится в некоторой инерциальной системе отсчета; 2) пружина динамометра растягивается равномерно по всей длине. Проще всего эти два условия обеспечиваются равенством сил, действующих на оба конца пружины динамометра. В важности второго условия нетрудно убедиться с помощью следующего рассуждения. Допустим, мы закрепили одну половину пружины (соединенную со шкалой) так, что она вообще не будет деформироваться и перемещаться, а за свободный конец второй половины пружины тянем с силой F (рис. 1). Что в этом случае покажет динамометр? Очевидно, половина пружины под действием силы F удлинится на столько же, на сколько удлинится вся пружина под действием силы F/2. Таким образом, стрелка динамометра покажет силу F/2.
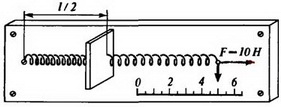
Рис. 1.
Итак, если сила натяжения постоянна вдоль пружины и равна F, динамометр покажет F. Если же сила натяжения равна нулю на одной половине пружины и F на другой, динамометр покажет F/2. А что если сила натяжения будет изменяться вдоль пружины еще каким-нибудь, более сложным образом? Какой будет суммарная деформация всей пружины (ведь именно она «ответственна» за показание стрелки динамометра)? Как, наконец, создать неравномерную силу натяжения, не закрепляя части пружины?
Оказывается, в условиях задачи 3 реализуется именно такая ситуация. Так что же происходит, если сила F действует только на один конец динамометра?
Во-первых, динамометр движется и движется равноускоренно (других сил нет). Его ускорение равно 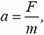 где m — масса пружины. При таком движении взаимное расположение точек пружины не изменяется со временем. Можно сказать, что пружина движется как твердое тело (при условии, разумеется, что возможные продольные колебания быстро затухают). При этом взаимное расположение точек движущейся пружины может, конечно, отличаться от их расположения в неподвижном состоянии.
где m — масса пружины. При таком движении взаимное расположение точек пружины не изменяется со временем. Можно сказать, что пружина движется как твердое тело (при условии, разумеется, что возможные продольные колебания быстро затухают). При этом взаимное расположение точек движущейся пружины может, конечно, отличаться от их расположения в неподвижном состоянии.
Во-вторых, различные участки пружины будут деформироваться по-разному, поскольку сила натяжения будет изменяться вдоль пружины. Определим эту силу, считая, что пружина расположена горизонтально и сила F действует на ее правый конец.
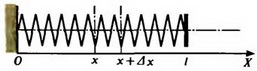
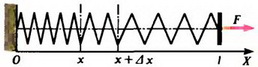
Для дальнейшего удобства «пронумеруем» точки (витки) пружины с помощью непрерывно изменяющейся величины x следующим образом (рис. 2).
а
б
Рис. 2.
Вместо того, например, чтобы говорить «точка пружины, которая находится на расстоянии x от левого конца пружины в недеформированном состоянии», будем говорить кратко «точка x». Очевидно, что x изменяется в пределах от 0 до l, где l — длина недеформированной пружины. Силу натяжения в точке x обозначим F(x); при этом понятно, что F(0) = 0 и F(l) = F. Заметим, что масса участка пружины от точки 0 до точки x равна 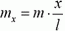 . Для того чтобы этот участок двигался с ускорением
. Для того чтобы этот участок двигался с ускорением 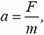 необходимо, чтобы на него со стороны остальной части пружины действовала сила — сила натяжения в точке x —
необходимо, чтобы на него со стороны остальной части пружины действовала сила — сила натяжения в точке x —
Эта сила линейно зависит от параметра точки пружины x (рис. 3).
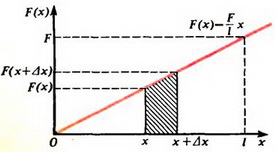
Рис. 3.
Теперь задача сводится к тому, чтобы, зная силу натяжения в каждой точке пружины, определить деформацию всей пружины. Для этого поступим так. Выделим малый (по сравнению с l) участок недеформированной пружины между точками x и x + Δх (рис. 2, а). Длину этого участка Δx будем обозначать также b. На левый конец этого участка действует сила натяжения 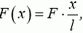 на правый — сила натяжения
на правый — сила натяжения 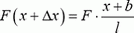 . Равнодействующая этих сил, направленных в разные стороны, равна
. Равнодействующая этих сил, направленных в разные стороны, равна 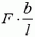 . Поскольку масса выделенного участка есть
. Поскольку масса выделенного участка есть 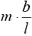 , он движется с ускорением, равным
, он движется с ускорением, равным 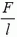 , т. е. с ускорением всей пружины.
, т. е. с ускорением всей пружины.
Так как силы 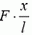 и
и 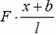 отличаются на малую (по сравнению с ними) величину
отличаются на малую (по сравнению с ними) величину 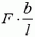 , можно считать, что участок Δx растягивают в обе стороны с силой
, можно считать, что участок Δx растягивают в обе стороны с силой 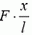 , под действием которой он деформируется. Найдем величину абсолютного удлинения этого участка.
, под действием которой он деформируется. Найдем величину абсолютного удлинения этого участка.
Если бы на оба конца пружины действовала сила F0, в каждой точке x сила натяжения также равнялась бы F0, и пружина была бы растянута равномерно. Абсолютное удлинение всей пружины было бы равно
где k — жесткость пружины, а относительное удлинение —
При этом относительное удлинение любого участка было бы таким же.
Например, для участка длиной b
В случае же, когда сила натяжения зависит от x, относительное удлинение участка длиной b будет другим:
Это означает, что участки возле правого конца пружины растягиваются больше, возле левого — меньше (см. рис. 2, б и рис. 4).

Рис. 4.
Абсолютное удлинение этого участка есть
Заметим, что величина абсолютного удлинения участка Δx, с точностью до постоянного коэффициента 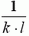 равна площади прямоугольника со сторонами F(x) и Δx или F(x + Δx) и Δx (см. рис. 3). Ясно, что в пределе (для бесконечно малых Δx) силы F(x) и F(x + Δx) совпадают, а площади указанных прямоугольников равны как между собой, так и площади заштрихованной на рисунке 3 трапеции.
равна площади прямоугольника со сторонами F(x) и Δx или F(x + Δx) и Δx (см. рис. 3). Ясно, что в пределе (для бесконечно малых Δx) силы F(x) и F(x + Δx) совпадают, а площади указанных прямоугольников равны как между собой, так и площади заштрихованной на рисунке 3 трапеции.
Для того чтобы найти абсолютное удлинение всей пружины, разделим ее на n кусков малой длины точками x1 = 0, x2, …, xn, xn+1 = l. Будем считать, что
(n велико). Абсолютное удлинение i-гo участка выразится формулой
а абсолютное удлинение всей пружины —
Устремим теперь длину каждого участка к нулю (а их число к бесконечности). Тогда получим
Ясно, что эта сумма, с точностью до коэффициента ![]() , равна сумме площадей трапеций, подобных заштрихованной на рисунке 3, а ее предел — площади прямоугольного треугольника с катетами F и l. Следовательно,
, равна сумме площадей трапеций, подобных заштрихованной на рисунке 3, а ее предел — площади прямоугольного треугольника с катетами F и l. Следовательно,
Для тех, кто знаком с понятием определенного интеграла, запишем
Итак, абсолютное удлинение Δl всей пружины, на один конец которой действует сила F, найдено. Можно сказать, что это удлинение будет таким же, если на оба конца динамометра действует так называемая эффективная сила 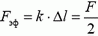 . Но, как уже говорилось, если на оба конца динамометра действуют одинаковые силы, динамометр показывает именно ее. Таким образом, если на один конец динамометра действует сила F, то динамометр показывает силу F/2 (и движется равноускоренно). При этом заметим, что показание динамометра не зависит ни от массы m пружины, ни от ее длины l в свободном состоянии, ни от жесткости k.
. Но, как уже говорилось, если на оба конца динамометра действуют одинаковые силы, динамометр показывает именно ее. Таким образом, если на один конец динамометра действует сила F, то динамометр показывает силу F/2 (и движется равноускоренно). При этом заметим, что показание динамометра не зависит ни от массы m пружины, ни от ее длины l в свободном состоянии, ни от жесткости k.
Разобравшись с задачей 3, вернемся к задаче 1. Если на правый конец динамометра действует сила F1, а на левый F2, то пружина движется с ускорением
Для участка пружины от 0 до x имеем
следовательно, сила натяжения в точке x равна
Абсолютное удлинение можно найти с помощью тех же рассуждений, что и раньше. Так, с одной стороны, абсолютное удлинение пружины равно площади заштрихованной на рисунке 5 трапеции (деленной на k·l).
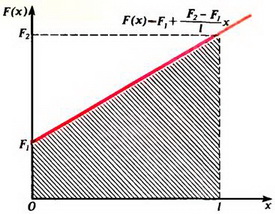
Рис. 5.
С другой стороны, его можно выразить в виде интеграла:
Таким образом, динамометр, на концы которого действуют различные силы F1 и F2 растягивается так, как если бы на оба его конца действовала одна и та же сила 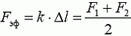 . Другими словами, динамометр показывает (независимо от величин m, l и k) силу, равную полусумме F1 и F2, и движется при этом равноускоренно. В частном случае, когда F1 = 0, мы получим результат задачи 3:
. Другими словами, динамометр показывает (независимо от величин m, l и k) силу, равную полусумме F1 и F2, и движется при этом равноускоренно. В частном случае, когда F1 = 0, мы получим результат задачи 3: 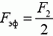 . В другом частном случае, когда F1 = F2 = F, имеем Fэф = F, т. е. когда силы, действующие на оба конца динамометра, одинаковы, динамометр, как и должно быть, показывает именно эту силу и покоится.
. В другом частном случае, когда F1 = F2 = F, имеем Fэф = F, т. е. когда силы, действующие на оба конца динамометра, одинаковы, динамометр, как и должно быть, показывает именно эту силу и покоится.
Теперь рассмотрим задачу 2. Так можно ли сделать какие-нибудь измерения с помощью одного только динамометра? Оказывается, можно. Сначала расположим динамометр горизонтально и убедимся, что его стрелка находится на нулевом делении. Затем расположим динамометр вертикально, держа за верхний конец пружины, который прикреплен к шкале. В таком положении стрелка динамометра (нижний конец пружины) покажет не ноль — пружина растянется под действием силы тяжести. Но на сколько? Что же теперь покажет динамометр?
Заметим, что в вертикальном положении на концы пружины действуют различные силы. На верхнем конце сила натяжения пружины равна mg, где m — масса пружины, на нижнем сила натяжения равна нулю. Кроме того, сила натяжения на расстоянии x от нижнего конца пружины равна 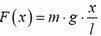 (покажите). Но тогда ситуация такая же, как и в задачах 1 и 3. Воспользовавшись их результатами, находим, что динамометр покажет эффективную силу
(покажите). Но тогда ситуация такая же, как и в задачах 1 и 3. Воспользовавшись их результатами, находим, что динамометр покажет эффективную силу 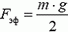 .
.
Вывод: масса пружины динамометра равна 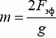 , где Fэф — показания динамометра в вертикальном положении.
, где Fэф — показания динамометра в вертикальном положении.
В заключение — несколько задач для самостоятельного решения.
Упражнения
1. Динамометр подвешен вертикально за верхний конец (за который пружина прикреплена к шкале). К его нижнему концу подвешен (верхним концом) второй динамометр, а к нижнему концу второго — третий. Все динамометры одинаковые. Верхний динамометр показывает силу F. Что показывают второй и третий динамометры? Массой шкал пренебречь.
2. Пружина в горизонтальном положении имеет длину 1 м. Подвешенная за один конец, она растягивается до 1,2 м. Другая такая же пружина имеет в горизонтальном положении длину 2 м. До какой длины она растянется, если ее тоже подвесить за один конец?
3. Пружина динамометра может как растягиваться, так и сжиматься, подчиняясь в обоих случаях закону Гука. За один конец динамометра тянут с силой 70 Н, другой толкают в том же направлении с силой 50 Н. Что покажет динамометр?
4. Стержень, изготовленный из упругого материала (металл, резина), аналогичен пружине. Если на его торцы действуют одинаковые растягивающие силы F, то относительное удлинение стержня равно 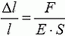 , где S — площадь поперечного сечения стержня, E — коэффициент, зависящий от свойств материала (модуль Юнга). Какой должна быть длина стального стержня в горизонтальном положении, чтобы при подвешивании его за один конец длина стержня увеличилась на 1 мм? Для стали E = 2,1·106 Н/мм2, плотность ρ = 7,8·103 кг/м3.
, где S — площадь поперечного сечения стержня, E — коэффициент, зависящий от свойств материала (модуль Юнга). Какой должна быть длина стального стержня в горизонтальном положении, чтобы при подвешивании его за один конец длина стержня увеличилась на 1 мм? Для стали E = 2,1·106 Н/мм2, плотность ρ = 7,8·103 кг/м3.
5. Стальной стержень (см. предыдущую задачу), поставленный «на попа», имеет длину 1 м. Какой будет длина стержня, если его подвесить за верхний конец?
Ответы
1) 3F/5; F/5. 2) 2,8 м. 3) 10 H. 4) 74,1 м. 5) 1 + 3,6·10-7 м.
| Выложил | alsak |
| Опубликовано | 11.02.09 |
| Просмотров | 28224 |
| Рубрика | Решение задач |
| Тема | Динамика |