Сакович А.Л. Движение под действием нескольких сил. Механика. Рекомендации по решению задач-2/2
Сакович А.Л. Движение под действием нескольких сил. Механика. Рекомендации по решению задач // Фiзiка: праблемы выкладання. – 2008. – № 6. – С. 25-34.
Авторский вариант.
Продолжение
Операции, связанные с указанием направления скорости и ускорения, должны были быть отработаны еще в кинематике, поэтому в данной статье рассматриваться не будут. В качестве напоминания можно предложить учащимся следующее.
При прямолинейном движении ускорение направлено:
- в сторону движения (скорости), если скорость тела увеличивается;
- в противоположную сторону движения (скорости), если скорость тела уменьшается.
При равномерном движении по окружности тело движется с центростремительным ускорением, направленным к центру окружности.
Следующие элементарные операции связаны с построением чертежа. Здесь следует обратить внимание на такие правила:
- Большинство тел в динамике – это материальные точки, которые изображаются в виде прямоугольников или окружностей.
- Сила изображается в виде направленного отрезка, начало которого расположено в точке приложения силы.
- Силы, действующие на материальные точки, будем изображать из середины тела.
- Равнодействующая всех действующих сил должна быть направлена в сторону ускорения.
Для закрепления полезно разобрать задачи, в которых тела движутся по вертикали, горизонтально и по окружности.
Задачи на закрепление
10. Автомобиль движется по горизонтальной дороге. Изобразите все действующие на автомобиль силы, укажите направления скорости и ускорения, когда он: а) увеличивает свою скорость; б) тормозит.
Решение. Автомобиль взаимодействует с дорогой и Землей (по умолчанию), следовательно, на него будут действовать: 1) сила реакции опоры дороги (N), направленная вверх перпендикулярно поверхности; 2) сила тяжести (m∙g), направленная вертикально вниз; 3) сила трения (сила сопротивления) (Fтр), направленная вдоль поверхности против скорости; 4) сила тяги (F), направленная в сторону движения (по умолчанию).
Определим направления ускорений в каждом случае: а) автомобиль увеличивает свою скорость, следовательно, ускорение направлено в сторону скорости; б) автомобиль тормозит, следовательно, ускорение направлено в противоположную сторону скорости.
Обратите внимание, что на всех рисунках N = m∙g, т.к. автомобиль не движется с ускорением по вертикали. На рис. 16 а силы изображены так, чтобы Fтр < F, т.к. ускорение направлено в сторону силы тяги (движения); на рис. 16 б Fтр > F, т.к. ускорение направлено в сторону Fтр (против движения).
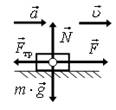
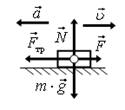
а б
Рис. 16.
11. Велосипедист равномерно движется по дороге. Изобразите все действующие на велосипедиста силы, укажите направления скорости и ускорения, когда он: а) проходит середину выпуклого моста; б) проходит середину вогнутого моста.
Решение. Велосипедист взаимодействует с дорогой и Землей (по умолчанию), следовательно, на него будут действовать: 1) сила реакции опоры дороги (N), направленная вверх перпендикулярно поверхности; 2) сила тяжести (m∙g), направленная вертикально вниз; 3) сила трения (сила сопротивления) (Fтр), направленная вдоль поверхности против скорости; 4) сила тяги (F), направленная в сторону движения (по умолчанию).
При равномерном движении по окружности велосипедистдвижется с центростремительным ускорением, направленным к центру окружности.
Обратите внимание, что на всех рисунках Fтр = F, т.к. велосипедистдвижется равномерно по дороге, ускорения вдоль оси 0Х нет. На рис. 17 а силы изображены так, чтобы m∙g > N, т.к. ускорение направлено вниз (к центру окружности); на рис. 17 б – m∙g < N, т.к. вверх (к центру окружности).
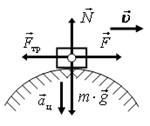
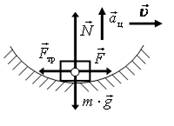
а б
Рис. 17.
Особое внимание необходимо обратить на движение взаимодействующих тел.
12. Аэросани массой М равномерно тянут прицеп (сани) массой m по горизонтальной дороге. Сила тяги аэросаней F. Изобразите силы взаимодействия между следующими телами: Земля, аэросани, сани, дорога.
Решение. Рассмотрим взаимодействующие пары тел.
Земля – сани. Сила, возникающая в результате взаимодействия этих тел, – это сила тяжести саней, которая направлены по вертикали. По третьему закону Ньютона, такая же по величине, но противоположная по направлению сила действуют и на Землю (рис. 18 а).
Земля – аэросани. Сила, возникающая в результате взаимодействия этих тел, – сила тяжести аэросаней, которая направлены по вертикали. По третьему закону Ньютона, такая же по величине, но противоположная по направлению сила действуют и на Землю (рис. 18 б).
Дорога – сани. Сани давят на дорогу – это вес саней, дорога действует на сани – это сила реакции опоры. Эти силы направлены перпендикулярно дороге. Так как сани движутся (скользят), то между санями и дорогой действует так же сила трения скольжения, направленная вдоль поверхности против движения саней. По третьему закону Ньютона, такая же по величине, но противоположная по направлению сила действуют и на дорогу (рис. 18 в).
Дорога – аэросани. Аэросани давят на дорогу – это вес аэросаней, дорога действует на аэросани – это сила реакции опоры. Эти силы направлены перпендикулярно дороге. Так как аэросани движутся (скользят), то между аэросанями и дорогой действует так же сила трения скольжения, направленная вдоль поверхности против движения аэросаней. По третьему закону Ньютона, такая же по величине, но противоположная по направлению сила действуют и на дорогу (рис. 18 г).
Аэросани – сани. Аэросани действуют на сани при помощи сцепки, которая растягивается. Поэтому на сани и на аэросани действуют силы упругости сцепки, направленные вдоль сцепки, в но противоположные стороны ее растяжения (рис. 18 д).
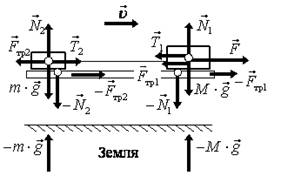
На рис. е указаны все тела данной задачи и изображены все действующие силы. На аэросани действует также сила тяги F. ОБРАТИТЕ ВНИМАНИЕ, что для наглядности рисунка, линии действия некоторых сил не совпадают.
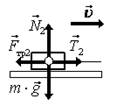
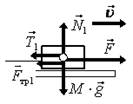
При решении задач нужно выделять силы, действующие на отдельные тела. Силы, действующие только на сани, изображены на рис. 18 ж; силы, действующие только на аэросани, изображены на рис. 18 з; силы, действующие только на дорогу, изображены на рис. 18 и.
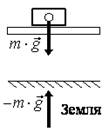
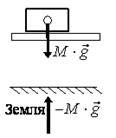
а б
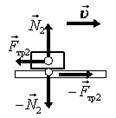
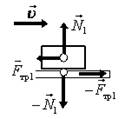
в г

д
е
ж з
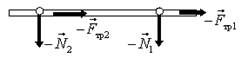
и
Рис. 18.
Обобщим выделенные элементарные операции, в результате получив следующий расширенный план первого пункта:
1.1. Сделайте чертеж, на которых тела изобразите в виде прямоугольников (или окружностей).
1.2. Определите все действующие на тело силы.
1.3. Определите направление каждой силы.
1.4. Укажите направления скорости и ускорения.
1.5. Изобразите все действующие силы в виде направленных отрезков, начало которых расположено в середине тела (материальной точки).
2. Запишите второй закон Ньютона в векторном виде:
![]()
Используя один из способов решения, составьте систему уравнений. Проверьте, является ли полученная система уравнений полной. При необходимости воспользуйтесь дополнительными формулами.
При выполнении первой элементарной операции (запишите второй закон Ньютона в векторном виде) обычно, если правильно выполнен первый пункт плана, затруднений не бывает. Основная ошибка здесь в том, что эту операцию просто не выполняют, не видят необходимости или переоценивают свои способности при выполнении этого действия в уме.
Можно порекомендовать здесь такие трафареты:
![]()
(запишите справа все векторы сил, указанные на рисунке)
или
![]()
(оставьте только те силы, которые указаны на рисунке).
При составлении системы уравнений обычно используют только координатный метод решения. Хотя при решении задач, в которых силы направлены под углом ![]() к поверхности, иногда бывает проще решить задачу векторным способом.
к поверхности, иногда бывает проще решить задачу векторным способом.
Рассмотрим особенности координатного метода решения задач.
Здесь можно выделить такие элементарные операции:
1) выберите систему координат;
2) запишите второй закон Ньютона в проекциях на оси координат.
Все эти операции должны были быть отработаны еще в кинематике. При выборе системы координат можно порекомендовать направлять одну из осей вдоль ускорения или скорости, и проводить все оси через материальную точку. Все силы, направленных под углом к осям, желательно разложить на составляющие вдоль этих осей.
В качестве напоминания можно предложить учащимся следующее:
проекция вектора
- положительна, если составляющая вектора на данную ось направлена вдоль этой оси;
- отрицательна – если против оси;
- равнанулю – если вектор перпендикулярен оси.
Задачи на закрепление
13. На рис. 19 изображены тела, их ускорения, скорости, силы, действующие на эти тела, и оси координат. Запишите уравнения второго закона Ньютона для каждого тела в векторной форме и в проекциях на оси координат.
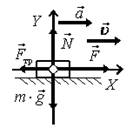
а
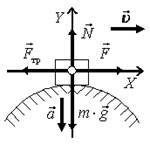
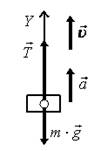
в
Рис. 19.
Решение а) Уравнение второго закона Ньютона в векторной форме имеет вид 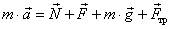 . Проекции этого уравнения
. Проекции этого уравнения
на ось 0Х: m∙ax = Nx + Fx + m∙gx + Fтр x, где m∙ax = m∙a, Nx = 0, Fx = F,
m∙gx = 0, Fтр x = –Fтр. Тогда m∙a = F – Fтр;
на ось 0Y: m∙ay = Ny + Fy + m∙gy + Fтр y, где m∙ay = 0, Ny = N, Fy = 0,
m∙gy = –m∙g, Fтр y = 0. Тогда 0 = N – m∙g.
б) Уравнение второго закона Ньютона в векторной форме имеет вид 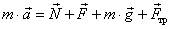 . Проекции этого уравнения
. Проекции этого уравнения
на ось 0Х: m∙ax = Nx + Fx + m∙gx + Fтр x, где m∙ax = 0, Nx = 0, Fx = F,
m∙gx = 0, Fтр x = –Fтр. Тогда 0 = F – Fтр;
на ось 0Y: m∙ay = Ny + Fy + m∙gy + Fтр y, где m∙ay = –m∙a, Ny = N, Fy = 0,
m∙gy = –m∙g, Fтр y = 0. Тогда –m∙a = N – m∙g или m∙a = m∙g – N.
в) Уравнение второго закона Ньютона в векторной форме имеет вид 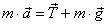 . Проекция этого уравнения
. Проекция этого уравнения
на ось 0Y: m∙ay = Ty + m∙gy, где m∙ay = m∙a, Ty = T, m∙gy = –m∙g. Тогда
m∙a = T – m∙g.
14. Запишите уравнения второго закона Ньютона в векторной форме и для проекций на оси координат для тела, изображенного на рис. 20.
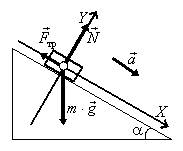
Рис. 20.
Решение. Уравнения второго закона Ньютона в векторном виде: 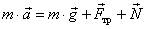 . Разложим вектор
. Разложим вектор 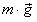 на две составляющее
на две составляющее 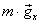 и
и 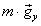 . Тогда проекции этого уравнения (рис. 21):
. Тогда проекции этого уравнения (рис. 21):
0X: m∙ax = m∙gx + Fтр x+ Nx, где m∙ax = m∙a, m∙gx = m∙g·sinα, Fтр x = –Fтр,
Nx = 0. Тогда m∙a = m∙g·sinα– Fтр.
0Y: m∙ay = m∙gy + Fтр y + Ny, где m∙ay = 0, m∙gy = –m∙g·cosα, Fтр y = 0,
Ny = N. Тогда 0 = N – m∙g∙cosα.
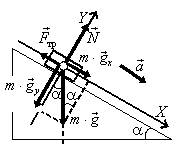
Рис. 21.
Векторный метод решения
Векторный методизучается в ознакомительном порядке.
Второй закон Ньютона связывает между собой векторные величины 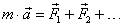 (1), поэтому некоторые задачи динамики можно решать векторным методом, т.е. геометрическим суммированием векторов.
(1), поэтому некоторые задачи динамики можно решать векторным методом, т.е. геометрическим суммированием векторов.
Наиболее эффективен этот метод в случаях, когда второй закон Ньютона (или в преобразованном виде) связывает между собой три вектора.
Одной из операций векторного метода является построение векторного многоугольника сил. Для ее закрепления можно предложить упражнения следующего вида.
15. Тело массы т под действием трех сил 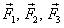 движется равномерно (а = 0) (рис. 22). Постройте векторный многоугольник сил.
движется равномерно (а = 0) (рис. 22). Постройте векторный многоугольник сил.
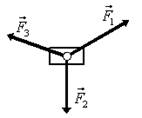
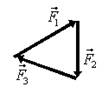
Рис. 22. Рис. 23.
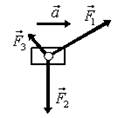
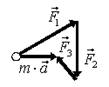
Рис. 24. Рис. 25.
Решение.Запишемвторой закон Ньютона: 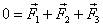 . Векторный многоугольник сил для этого уравнения изображен на рис. 23.
. Векторный многоугольник сил для этого уравнения изображен на рис. 23.
16. Тело массы т под действием трех сил 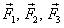 движется с ускорением
движется с ускорением 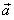 (рис. 24). Постройте векторный многоугольник сил.
(рис. 24). Постройте векторный многоугольник сил.
Решение.Запишемвторой закон Ньютона: 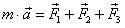 . Векторный многоугольник сил для этого уравнения изображен на рис. 25.
. Векторный многоугольник сил для этого уравнения изображен на рис. 25.
В некоторых случаях можно преобразовывать второй закон Ньютона, уменьшая число векторов. Делают это за счет вспомогательного построения сумм двух-трех векторов, причем так, чтобы значение результирующего вектора можно было легко рассчитать.
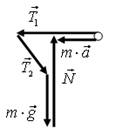
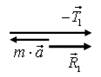
а б
в г
Рис. 26.
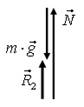
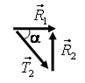
Например, многоугольник сил 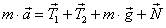 , изображенный на рис. 26 а, можно упростить следующим образом
, изображенный на рис. 26 а, можно упростить следующим образом 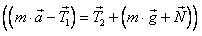 : 1) найти разность векторов
: 1) найти разность векторов 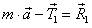 (рис. 26 б); 2) найти сумму векторов
(рис. 26 б); 2) найти сумму векторов 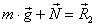 (рис. 26 в). Тогда получим следующий многоугольник сил
(рис. 26 в). Тогда получим следующий многоугольник сил 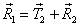 (рис. 26 г).
(рис. 26 г).
Следующей операцией является запись уравнений. Это полностью геометрическая задача. Например, пусть в предыдущем примере заданы следующие величины: т = 2 кг, а = 7 м/с2, Т1 = 30 Н, N = 40 Н, и надо найти значение и направление вектора 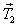 .
.
Решение. Найдем значения 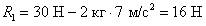 (см. рис. 26 б),
(см. рис. 26 б), 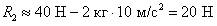 (см. рис. 26 в). Из прямоугольного треугольника (см. рис. 26 г) находим
(см. рис. 26 в). Из прямоугольного треугольника (см. рис. 26 г) находим 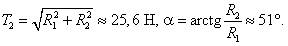 .
.
Задачи на закрепление
17. Запишите уравнение второго закона Ньютона для шарика в векторной форме (рис. 27). Используя векторный метод решения, запишите уравнение, связывающее между собой массу шарика m, длину нити l, угол a и скорость вращения шарика.
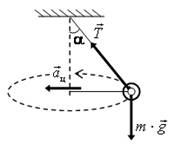
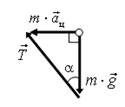
Рис. 27. Рис. 28.
Решение. Запишем второй закон Ньютона 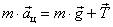 . Векторный многоугольник (прямоугольный треугольник) сил для уравнения изображен на рис. 28. При движении по окружности в горизонтальной плоскости шарик обладает центростремительным ускорением
. Векторный многоугольник (прямоугольный треугольник) сил для уравнения изображен на рис. 28. При движении по окружности в горизонтальной плоскости шарик обладает центростремительным ускорением 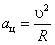 , где
, где 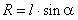 . Из прямоугольного треугольника получаем
. Из прямоугольного треугольника получаем
.
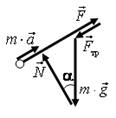
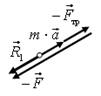
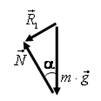
18. Запишите уравнения второго закона Ньютона в векторной форме для бруска, изображенного на рис. 29. Используя векторный метод решения, запишите уравнение, связывающее между собой величины, указанные на рисунке.
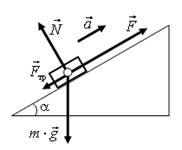
Рис. 29.
Решение. Уравнения второго закона Ньютона в векторном виде 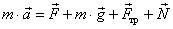 . Векторный многоугольник сил для уравнения изображен на рис. 30 а. Упростим данный многоугольник сил
. Векторный многоугольник сил для уравнения изображен на рис. 30 а. Упростим данный многоугольник сил 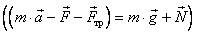 , для этого найдем сумму векторов
, для этого найдем сумму векторов 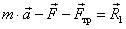 или
или 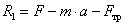 (рис. 30 б). Тогда получим следующий многоугольник сил
(рис. 30 б). Тогда получим следующий многоугольник сил 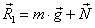 (рис. 30 в). Из прямоугольного треугольника получаем
(рис. 30 в). Из прямоугольного треугольника получаем
или
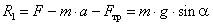 , или
, или 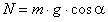 и т.п.
и т.п.
а б в
Рис. 30.
Выделим еще несколько элементарных операций в алгоритме решения:
1) проверьте, является ли полученная система уравнений полной;
2) при необходимости воспользуйтесь дополнительными формулами.
Систему уравнений будем считать полной, если ее решение позволит получить соотношение между требованием и условием задачи. Одним из критериев полноты системы может служить следующее: число уравнений должно быть не меньше числа неизвестных величин. Эта операция отрабатывается на уроках алгебры, и в данной статье рассматриваться не будет.
К дополнительным формулам отнесем расчетные формулы, которые рассматривались выше:
- сила гравитационного взаимодействия –
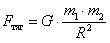 ;
;
- сила тяжести –
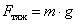 или
или 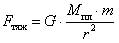 ;
;
- сила упругости –
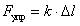 или
или 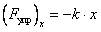 , или
, или 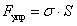 ;
;
- силы сухого трения –
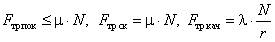 ;
;
- сила сопротивления –
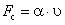 или
или 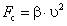 ;
;
- архимедова сила –
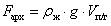 .
.
Так же можно применять и кинематические формулы (для движущего тела) и специальные условия, заданные в задаче.
Обобщим выделенные элементарные операции, в результате получив следующий расширенный план второго пункта:
2.1. Запишите второй закон Ньютона в векторном виде.
2.2. Составьте систему уравнений.
Для координатного метода решения:
2.2.1. Выберите систему координат.
2.2.2. Запишите второй закон Ньютона в проекциях на оси координат.
Для векторного метода решения:
2.2.3. При необходимости сделайте преобразование второго закона Ньютона.
2.2.4. Постройте векторный многоугольник сил.
2.2.5. Запишите уравнения.
2.3. Проверьте, является ли полученная система уравнений полной.
2.4. При необходимости воспользуйтесь дополнительными формулами.
3. Решите полученные уравнения
Эта операция отрабатывается на уроках математики, и в данной статье рассматриваться не будет.
Рекомендую при проверке задач, решенных по расширенном плану, фиксировать выполнение каждой элементарной операции отдельно. Это позволит определить какому ученику над какой операцией еще необходимо поработать, а какому можно уже выполнять отдельные операции в уме.
Рассмотрим пример решения задачи по расширенному плану.
19. При проведении лабораторной работы были получены следующие данные: длина наклонной плоскости 1 м, высота 20 см, масса деревянного бруска 200 г, сила тяги, измеренная динамометром при равномерном движении бруска вверх, 1 Н. Найдите коэффициент трения.
Решение.
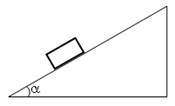
1.1. Сделайте чертеж, на которых тела изобразите в виде прямоугольников (или окружностей).
Чертеж изображен на рис. 31 а.
а
б
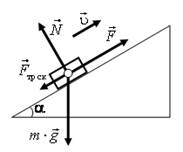
Рис. 31.
1.2. Определите все действующие на тело силы.
Брусок взаимодействует с твердой поверхностью наклонной плоскости, которая под действием веса бруска будет деформироваться, с воздухом и с Землей (по умолчанию). Поэтому на брусок будут действовать: 1) сила реакции опоры доски (N) (со стороны деформированной поверхности стола); 2) сила тяжести (m∙g) (со стороны Земли); 3) сила трения скольжения (Fтр) (со стороны твердой поверхностью стола); 4) сила тяги (F). Архимедовой силой (со стороны воздуха) пренебрегаем, т.к. плотность воздуха во много раз меньше плотности бруска.
1.3. Определите направление каждой силы.
Сила реакции опоры доски (N)направлена вверх перпендикулярно поверхности; сила тяжести (m∙g)– вертикально вниз; сила трения скольжения (Fтр) – вдоль поверхности против скорости; сила тяги (F) направлена в сторону движения (по умолчанию).
1.4. Укажите направления скорости и ускорения.
Скорость бруска направлена в сторону движения – вверх. Так как брусок движется равномерно, то ускорение равно нулю.
1.5. Изобразите все действующие силы в виде направленных отрезков, начало которых расположено в середине тела (материальной точки).
Все действующие силы и скорость указаны на рисунке 31 б.
2.1. Запишите второй закон Ньютона в векторном виде.
Второй закон Ньютона: 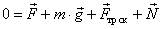 .
.
2.2. Составьте систему уравнений.
Для координатного метода решения
2.2.1. Выберите систему координат.
Направим ось 0Х вдоль скорости (поверхности), тогда ось 0Y вверх, перпендикулярно поверхности (рис. 32 а).
2.2.2. Запишите второй закон Ньютона в проекциях на оси координат.
Разложим вектор 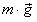 на две составляющее
на две составляющее 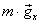 и
и ![]() . Тогда проекции этого уравнения (рис. 32 б):
. Тогда проекции этого уравнения (рис. 32 б):
0X: 0 = F – m∙g·sinα– Fтр ск (1), 0Y: 0 = N – m∙g·cosα(2).
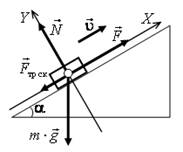
а
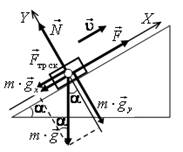
б
Рис. 32.
Для векторного метода решения
2.2.3. При необходимости сделайте преобразование второго закона Ньютона.
Преобразуем второй закон Ньютона следующим образом: 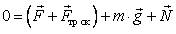 , для этого найдем сумму векторов
, для этого найдем сумму векторов 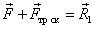 или
или 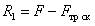 (рис. 33 а). Тогда получаем
(рис. 33 а). Тогда получаем 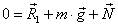 .
.
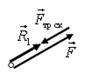
2.2.4. Постройте векторный многоугольник сил.
Векторный многоугольник сил 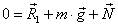 (рис. 33 б).
(рис. 33 б).
2.2.5. Запишите уравнения.
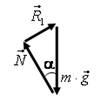
Из прямоугольного треугольника (см. рис. 33 б) получаем
![]() (3)
(3)
или
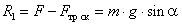 (4),
(4),
или
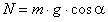 (5).
(5).
а б
Рис. 33.
2.3. Проверьте, является ли полученная система уравнений полной.
Данные системы уравнений не являются полными, т.к. ни система уравнений (1)-(2), ни система (3)-(5) не позволяют выполнить требование задачи «найдите коэффициент трения».
2.4. При необходимости воспользуйтесь дополнительными формулами.
Воспользуемся еще несколькими уравнениями
![]() .
.
3. Решите полученные уравнения.
Для координатного метода решения
Решим систему уравнений (1)-(2) и (6)-(8). Например
0 = F – m∙g·sinα– μ∙m∙g·cosα, μ∙m∙g·cosα = F – m∙g·sinα,
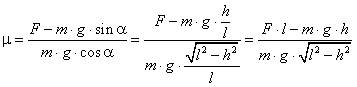 , μ≈ 0,32.
, μ≈ 0,32.
Для векторного метода решения
Решим систему уравнений (4)-(8). Например
![]()
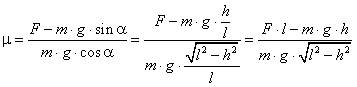 , μ≈ 0,32.
, μ≈ 0,32.
Литература
1. Каменецкий С.Е., Орехов В.П. Методика решения задач по физике в средней школе. – М.: Просвещение, 1987. – 336 с.
2. Луцевич А.А., Яковенко С.В. Физика: Учебн. пособие. – Мн.: Выш. шк., 2000. – 495 с.
3. Усова А.В., Тулькибаева Н.Н. Практикум по решению физических задач. – М.: Просвещение, 1992. – 208 с.
4.Физика. Механика. 10 кл.: Учеб. для углубленного изучения физики /Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
5.Физика. Теория и технология решения задач /Под общ. ред. В.А. Яковенко. – Мн.: ТетраСистемс, 2003. – 560 с.
| Выложил | alsak |
| Опубликовано | 14.12.08 |
| Просмотров | 23871 |
| Рубрика | Методика | Решение задач |
| Тема | Динамика |