Давиденко А.А. Рационализаторские задачи
Давиденко А.А. Рационализаторские задачи // Фiзiка: праблемы выкладання. – 2003. – № 5. – С. 72-77.
При постановке рационализаторских задач обязательно следует обращать внимание на то, чтобы они не были надуманными, а возникали из потребностей человека. В связи с этим для развития творческих способностей школьников необходимо использовать наиболее знакомые для них ситуации: уроки, занятия в школьных кружках и кружках центров научного и технического творчества ученической молодежи (станций юных техников), кружках соответствующих секций территориальных отделений Малой академии наук и т.п.
Слово рационализация происходит от латинского rationalis– умный и означает организацию любой деятельности более целесообразными, по сравнению с уже существующими, способами, улучшение, усовершенствование чего-либо [9, с. 569].
Если это усовершенствование будет осуществляться техническим способом [8, с. 156], то мы будем иметь дело с решением рационализаторской задачи.
Рационализаторской следует считать такую задачу, вследствие технического решения которой достигается незначительное усовершенствование за счет изменения конструкции уже используемой техники или технологии. Это определение вытекает из самого понятия рационализаторского предложения [8, с. 132].
Психолог А.В.Антонов, который исследовал процесс изобретательской деятельности, утверждает, что «рационализаторское творчество в силу своего характера требует весьма невысокого уровня современных научных и научно-технических знаний и уж, конечно, не повышает этот уровень» [1, с. 20]. Очевидно, что к такому выводу он пришел с учетом существующей разницы между изобретением и рационализаторским предложением. Действительно, изобретение – новое и обладающее существенными отличиями техническое решение задачи, дающее положительный эффект [6; 8, с. 45]. В основе рационализаторского предложения также лежит техническое решение, но, как вытекает из приведенного выше определения, его уровень ограничивается незначительным усовершенствованием уже используемой техники или технологии за счет изменения ее конструкции.
Можно, конечно, частично согласиться с высказанным выше взглядом А.В. Антонова, но ни в коем случае не пренебрегать потенциальными возможностями рационализаторских задач относительно развития творческих способностей школьников. Важным в данном случае является то, что сам процесс обнаружения задачной ситуации, постановка проблемы и следующее формулирование рационализаторской задачи требуют от ученика таких психических качеств, как прозорливость, умение ощущать тонкие, невидимые извне сложные особенности окружающего мира, умение ощущать проблему, что имеет прямое отношение к характеристике творческой личности.
Следует обратить внимание на то, что научный и научно-технический уровень как изобретения, так и рационализаторского предложения определяется несколькими факторами объективного и субъективного характера (образование, профессионализм, место работы и т.п.). Тяжело, например, вообразить, чтобы человек, не понимая определенной технологии или же принципа действия конкретного устройства, мог увидеть существующую в них проблему и предложил путь ее решения. Видение проблемы, постановка и следующее возможное решение задачи наиболее продуктивно реализуются в знакомой для субъекта ситуации.
При постановке рационализаторских задач обязательно следует обращать внимание на то, чтобы результаты их решения вносили ощутимые положительные изменения в процесс жизнедеятельности человека. Такие задачи не должны быть надуманными. Они возникают из потребностей человека.
В связи с этим для развития творческих способностей школьников необходимо использовать наиболее знакомые для них ситуации: уроки, занятия в школьных кружках и кружках центров научного и технического творчества ученической молодежи (станций юных техников), кружках соответствующих секций территориальных отделений Малой академии наук и т.п.
Следует сказать, что проблемы, которые могут со временем привести к постановке рационализаторских задач, возникают на любых видах занятий по физике. Однако наиболее близкими в этом отношении все же являются уроки, на которых проводится демонстрационный или лабораторный эксперимент, решаются задачи, обсуждаются выполненные учениками технические проекты, научно-исследовательские роботы и т.п. Методика использования таких задач нашла свое отображение в ряде публикаций автора [4; 5 и др.].
Рассмотрим пример рационализаторской задачи, которая возникла во время выполнения учащимися лабораторного эксперимента. Заметим, что данная задача отразила известную учителям физики проблему, связанную с использованием в эксперименте грузов из набора НГМ-100. В результате действия внешних сил, что имеет место при соединении грузов, или же при их падении с определенной высоты на твердые подставки, их крючки довольно часто отламываются. Это делает грузы непригодными к дальнейшему использованию по назначению. В связи с этим можно прийти к постановке такой задачи.
Задача 1. Изготовленные литейным способом металлические грузы, которые используются в школьном физическом эксперименте, имеют один серьезный недостаток: их крючки достаточно часто отламываются. Вследствие этого они становятся непригодными для дальнейшего использования по назначению. Предложите, как можно восстановить эти грузы.
Решение. Способ восстановления груза виден из рисунка 1. Для этого сначала фрезой или напильником снимем из тела 1 груза остатки крючков и в точке пересечения диагоналей одной из подготовленных граней сверлом диаметром 2-2,5 мм просверлим сквозное отверстие 2. Потом подготовим кусок стального провода диаметром 2-2,2 мм и согнем на одном из его концов крючок. Такую заготовку 3 вставим в отверстие 2 (рис. 1, а). Для завершения процесса реставрации груза такой же крючок необходимо согнуть и на противоположном конце проволоки. Реставрированный груз изображен на рисунке 1, б. Понятно, что теперь он намного прочнее и не требует к себе такого бережного отношения, как тот, что был изготовлен в заводских условиях.
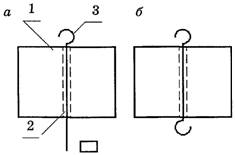
Рис. 1. Восстановление груза: 1 – груз; 2 – сквозное отверстие;
3 – заготовка из проволоки
Следующая рационализаторская задача возникла во время выполнения лабораторной работы по определению жесткости пружины. В формулировке данной задачи нашли отражение те неудобства, которые имеют место при одновременном измерении обычной линейкой величины деформации пружины и возникающей в ней силы упругости.
Задача 2. Одновременное измерение деформации пружины динамометра и силы упругости, которая возникает в пружине данного прибора, содержит неудобство: каждый раз приходится прикладывать линейку к его дощечке. Для соблюдения необходимой точности измерения удлинения пружины необходимо следить за предшествующим «выставлением нуля» линейки и достижением ее параллельности к шкале измерения силы.
Внесите предложение относительно конструктивных изменений основного для данной лабораторной работы прибора – динамометра, которые позволяли бы избежать этих недостатков.
Решение. Для облегчения процесса измерения удлинения пружины с одновременным повышением точности получаемого результата на дощечке динамометра целесообразно дополнительно поместить шкалу с миллиметровым и делениями (рис. 2).
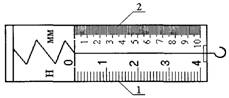
Рис. 2. Динамометр с дополнительной миллиметровой шкалой:
1 – шкала, проградуированная в ньютонах;
2 – шкала, проградуированная в миллиметрах
Очевидно, что совершенствоваться могут не только устройства, но и технологии. Технология – совокупность способов переработки материалов, изготовления изделий и процессы, которые сопровождают эти виды работ [9, с. 665]. Если под технологией, хотя бы условно, считать процесс выполнения лабораторной работы, ведь при этом используется совокупность способов и средств достижения поставленной цели (педагогическая технология), то можно сформулировать и следующую рационализаторскую задачу.
Задача 3. Предложенным в учебниках способом выполнения лабораторной работы «Измерение жесткости пружины» [2, с. 413–414; 8, с. 177–178] предполагается поочередно подвешивать на крючок пружины грузы с одновременным измерением удлинения пружины, что позволяет получать данные, на основе которых и достигается поставленная цель. Предложите, как можно усовершенствовать способ выполнения данной лабораторной работы.
Решение. Необходимые для выполнения данной лабораторной работы значения физических величин можно получить другим, отличающимся от предыдущего, способом. Расположим динамометр на столе. К его шкале приложим параллельно шкалу измерительной линейки так, чтобы совпадали их начала (нули). Деформируем действием руки пружину на определенную величину х1и одновременно снимем показания со шкалы динамометра. Это будет значение силы F1. Таким же способом получим значения х2,F2; х3,F3; х4,F4 и т.д. Дальнейший ход работы может быть таким, как это предложено в соответствующих учебниках.
Как видим, такая рационализация способа выполнения данной лабораторной работы позволяет обойтись без традиционно используемых штатива и грузов, что более выгодно с экономической точки зрения. Вместе с этим учащимся становится более очевидным, что деформация пружины первична, именно она вызывает возникновение силы упругости.
Ощутимых положительных результатов при таком способе выполнения лабораторной работы можно достичь путем использования описанного выше усовершенствованного динамометра, коэффициент жесткости пружины которого, а не жесткость, как способность тела или конструкции оказывать сопротивление деформированию [10, с. 31], мы и определяем. Здесь уже будет иметь место совмещение усовершенствования и оборудования и самого способа выполнения лабораторной работы, то есть технологии.
Следует заметить, что во время работы над решением рационализаторской задачи может возникнуть идея создания оригинального устройства, то есть может осуществиться логический переход к постановке и решению изобретательской задачи. Интересное решение изобретательской задачи может привести к конструированию и изготовлению изобретенного устройства и т.д. Такой процесс почти всегда имеет логическое продолжение и благоприятствует вовлечению учащихся в процесс научно-технического творчества.
1. Антонов А.Л. Психология изобретательского творчества. – Киев: Вища школа, 1978. – 175 с.
2. Гончаренко С.У. Фiзика. Проб. подручник для 9 кл. серед, загальноосвiт. шк., гiмназiй та кл. гуманiтарного профiлю. – К.: Освiта, 1997. – 431 с.
3. Давиденко А.А. Лабораторные работы в процессе обучения физике // Физика в школе. – 2000. – № 5. – С. 46–47; Фiзiка: праблемы выкладання. – 1997. – № 6. – С. 29–30.
4. Давиденко А.А. Учебные задания, максимально приближенные к жизненным ситуациям // Физика в школе. – 1990. – № 3. – С. 31–33.
5. Давиденко А.А. Залучення учнiв до удосконалення та розробки дослiдiв з фiзики / Збiрник наукових праць: Спецiльний випуск / В.Г.Кузь (гол. Ред.) та iн. – К.: Наук. Свiт, 2001. – С. 136–140.
6. Закон Украiни «Про охорону прав на винаходи i кориснi моделi» вiд 15 грудня 1993 р. № 3687-ХII. – В кн.: Закони Украiни. Т. 6., Киiв: Iнститут Законодавства, 1996. – С. 137–151.
7. Кикоин И.К., Кикоин A.К. Физика: Учеб. для 9 кл. сред, шк. – 2-е изд. – М.: Просвещение, 1992. – 191 с.
8. Прахов Б.Г. Изобретательство и патентоведение: Словарь-справочник. – Киев: Вища школа, 1987. – 182 с.
9. Словник iмшомовних слiв / За ред. О.С.Мельничука. – К.: Головна редакцiя УРЕ, 1974. – 776 с.
10. Физическая энциклопедия / Гл. ред. А.М.Прохоров. – М.: Сов. Энциклопедия. Т. II, 1990. – 703 с.
| Выложил | alsak |
| Опубликовано | 26.12.07 |
| Просмотров | 11591 |
| Рубрика | Экспериментальные задачи | Методика |
| Тема | Без тем |