Слободянюк А.И. Заметки о веревке 1/2
Слободянюк А.И. Заметки о веревке //Фiзiка: праблемы выкладання. – 2000. – № 1. – С. 75-77.
Ой, родная сторона,
сколь в тебе не рыскаю,
лобным местом ты красна
да веревкой склизкою.
В. Высоцкий
Введение. Если тяжелую гибкую веревку (или мягкую цепочку) подвесить за два конца к разным точкам, то она провиснет и примет форму линии, которая называется цепной. Многие даже слышали, что эта линия описывается «страшной» функцией — гиперболическим косинусом. Однако не многие знают, что это такое, и тем более почему именно этой функцией.
Эти заметки и посвящены одной интересной проблеме, связанной с провисающей веревкой и достаточно большим количеством задач на эту тему.
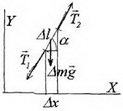
Небольшой парадокс.Выделим мысленно маленький участок провисающей веревки длиной Δl. Массу данного участка запишем в виде 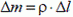 , где ρ – масса единицы длины веревки (линейная плотность). Пусть этот кусочек образует угол α с горизонтом. Так как он находится в равновесии, то сумма сил, действующих на него – натяжения веревки на его концах
, где ρ – масса единицы длины веревки (линейная плотность). Пусть этот кусочек образует угол α с горизонтом. Так как он находится в равновесии, то сумма сил, действующих на него – натяжения веревки на его концах 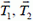 и сила тяжести
и сила тяжести 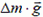 , равна нулю.
, равна нулю.
Запишем условие равновесия в проекции на направление выделенного участка:
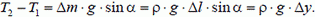 (1)
(1)
Таким образом, изменение силы натяжения веревки определяется изменением высоты ее концов. Более того, это утверждение можно распространить на участок произвольной длины (просто просуммировав выражения (1)) для всех маленьких кусочков.
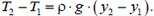 (2)
(2)
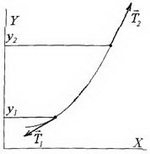
Не похоже ли на формулу для гидростатического давления?
Кстати, это соотношение широко используется при решении всевозможных задач.
Однако! Запишем условие равновесия в проекции на ось Y:
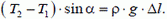 (3)
(3)
В этом уравнении нет ничего подобного на гидростатическое давление, да и противоречит оно соотношению (1)! Так какое же уравнение (1) или (3) верно?
См. продолжение.
| Выложил | alsak |
| Опубликовано | 07.06.09 |
| Просмотров | 9090 |
| Рубрика | Решение задач |
| Тема | Динамика Статика |