Два тела, связанные пружинкой, на наклонной плоскости.

[Lionel]

Пытаюсь решить задачу 2.4.22 из Савченко. Не получается никак, как учитывать то, что трение меняет направление при движении? Надо найти наибольшее удлинение пружины, трение есть только между верхним телом и плоскостью.
Вот условие.

[Lionel]

Спасибо, на dxdy подсказали решение. 
Здесь полное решение попробую написать, вдруг кому пригодится.

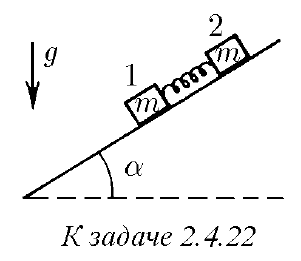
2.4.22 С наклонной плоскости, образующей угол α с горизонтом, начинают соскальзывать два тела массы m каждое, связанные первоначально недеформированной пружиной жесткости k. Определите наибольшее удлинение пружины, если трением между нижним телом и плоскостью можно пренебречь, а коэффициент трения между верхним телом и плоскостью равен µ.

Решение: Самое главное понять, что есть три случая.
1) Тело 2 начнет двигаться сразу.
2) Тело 2, вообще, не будет двигаться.
3) Тело 2 начнет двигаться не сразу,а  когда тело 1 пройдет какое-то расстояние, и пружина растянется.



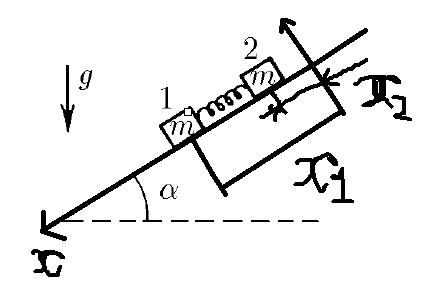
Запишем уравнения движения



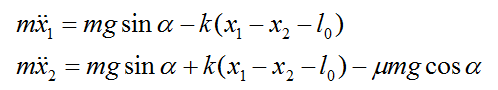l₀ это длина неформированной пружины, обозначим через x=x₁-x₂-l₀. Тогда вычитая уравнения получим.



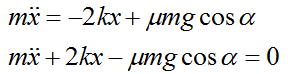
Проинтегрировав, получим



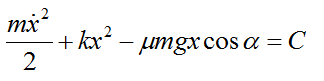
Где С это константа.
Теперь по случаям

1) Тело 2 начнет движение сразу, если



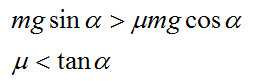
Тогда начальные условия такие,



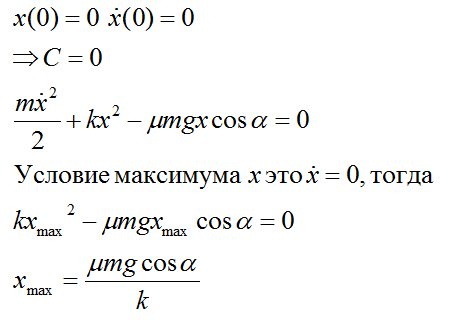2) Во втором случае, когда тело 2 не двигается вообще, тело 1 колеблется вокруг точки равновесия. Обозначим через y, его (тела 2)координату от первоначального положения (когда пружина недеформирована). Тогда



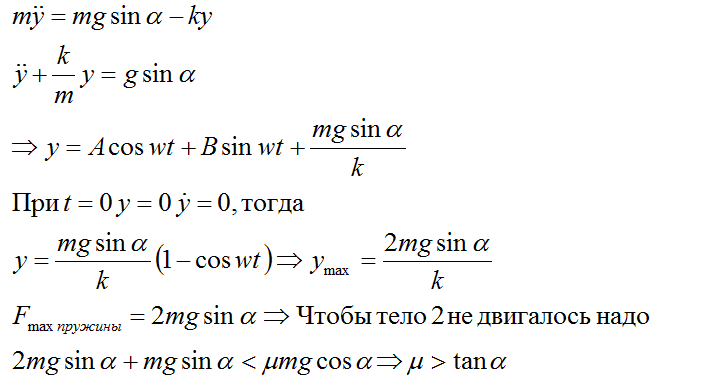3) Промежуточный случаи, когда коэффициент трения между tan a и 3 tan a




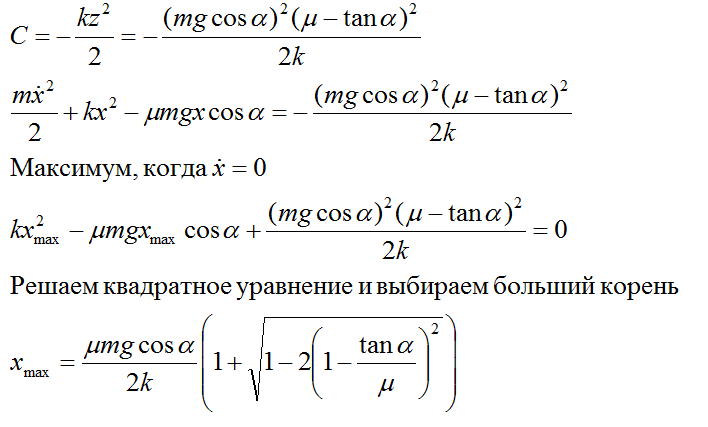
Вроде так.