Можаев В. Закон всемирного тяготения // Квант
Можаев В. Закон всемирного тяготения // Квант. — 1980. — №2. — С. 41-43.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Среди различных сил, действующих во Вселенной, самой фундаментальной и величественной является сила тяготения. Под действием этой силы планеты Солнечной системы, включая нашу Землю, движутся по своим орбитам вокруг Солнца. Эта сила притягивает к центру Земли все находящиеся на ней тела.
Против этой силы была направлена вся мощь двигателей космического корабля, когда 4 октября 1957 года впервые в мире на околоземную орбиту был выведен первый советский искусственный спутник Земли.
Первым, кто понял роль силы тяготения, был Ньютон. Анализируя законы Кеплера, которые описывают движение планет по своим орбитам вокруг Солнца, он пришел к заключению, что для удержания планеты на орбите должна существовать сила, направленная точно от планеты к Солнцу и обратно пропорциональная квадрату расстояния между ними. Однако главная заслуга Ньютона в том, что он сумел понять, что сила притяжения планеты к Солнцу — это частный случай силы тяготения, действующей между любыми двумя телами. Не случайно закон, открытый Ньютоном» называется законом всемирного тяготения. Это один из самых фундаментальных законов природы.
В простейшем случае, когда взаимодействующие тела можно считать материальными точками (размеры тел малы по сравнению с расстоянием между ними), закон всемирного тяготения формулируется так — любые две материальные точки притягивают друг друга с силой F, направленной по линии, их соединяющей, прямо пропорциональной их массам m1 и m2 и обратно пропорциональной квадрату расстояния r между ними:
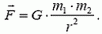 (*)
(*)
Здесь G = 6,67×10–11 Н·м2/кг2 — гравитационная постоянная; впервые она была измерена Кавендишем.
Если же размерами тел пренебречь нельзя, тела нужно мысленно разбить на небольшие участки такие, чтобы их можно было считать материальными точками. Для каждой пары материальных точек нужно записать закон тяготения в виде (*) и найти соответствующую силу притяжения, а затем — все полученные результаты сложить. Оказывается, для центрально симметричных тел (например, для шара или сферического слоя) силу притяжения можно считать непосредственно по формуле (*), понимая под r расстояние между центрами масс взаимодействующих тел.
Как известно, гравитационные поля (поля тяготения) являются потенциальными, то есть работа поля по перемещению тела из точки 1 в точку 2 не зависит от формы траектории, а определяется лишь разностью потенциальных энергий тела в точках 1 и 2 соответственно:
A12 = Ep1 – Ep2.
Из этого равенства ясно, что определенный физический смысл имеет лишь разность потенциальных энергий в различных точках поля. Численное же значение потенциальной энергии в отдельной точке особого смысла не имеет, оно всегда определяется с точностью до некоторой постоянной величины. Вот почему при решении конкретных задач нулевой уровень потенциальной энергии можно выбирать произвольно, в наиболее удобной точке.
Обычно для определения потенциальной энергии тела массой m. поднятого на высоту h над нулевым уровнем, пользуются формулой
Ep = m·g·h.
Однако это равенство справедливо лишь для значений h, много меньших радиуса Земли R3 (h « R3). Если такое условие не выполняется, потенциальную энергию надо считать, по-другому. Поясним это на конкретной задаче.
Задача 1. Полагая в бесконечности (то есть на большом расстоянии от Земли, где сила тяготения пренебрежимо мала) потенциальную энергию тела равной нулю, найдите зависимость потенциальной энергии Ep от расстояния r от центра Земли.
Ограничимся областью r ≥ R3.
Потенциальная энергия Ер тела массой m, находящегося на расстоянии r от центра Земли, равна работе, которую совершает поле тяготения, перемещая это тело из данной точки в бесконечность. Поскольку в потенциальном поле работа не зависит от формы траектории, будем считать, что тело перемещается вдоль радиального направления. При перемещении тела из точки 1, находящейся на расстоянии r1 от центра Земли (рис. 1), в точку 2, отстоящую от центра Земли на расстояние r2, поле совершает работу
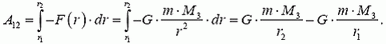
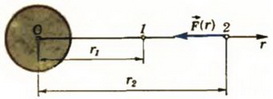
Рис. 1
При условии, что точка 2 бесконечно удалена, первое слагаемое равно нулю (при 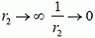 ). Таким образом, зависимость потенциальной энергии от расстояния r от центра Земли имеет вид
). Таким образом, зависимость потенциальной энергии от расстояния r от центра Земли имеет вид
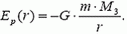
где М3 — масса Земли. График этой зависимости изображен на рисунке 2.
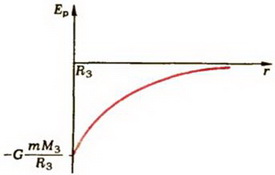
Рис. 2
Разберем еще несколько задач.
Задача 2. Определите, какую минимальную скорость надо сообщить находящемуся на поверхности Земли телу для того, чтобы оно ушло из сферы действия гравитационного ноля Земли.
Прежде всего заметим, что искомую скорость называют второй космической скоростью 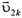 . Для определения ее модуля υ2k воспользуемся законом сохранения энергии.
. Для определения ее модуля υ2k воспользуемся законом сохранения энергии.
Сразу же после запуска, то есть непосредственно у поверхности Земли, кинетическая энергия тела равна 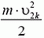 , а его потенциальная энергия равна
, а его потенциальная энергия равна 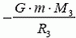 . Полная механическая энергия
. Полная механическая энергия
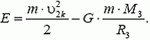
Когда тело удалится от Земли на бесконечно большое расстояние (уйдет за пределы действия поля тяготения Земли), потенциальная энергия тела станет равной нулю. Очевидно, что при этом кинетическая энергия тоже обратится в нуль (мы ищем минимальную начальную скорость тела). Поскольку полная энергия тела не изменяется, получаем
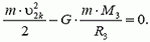
Отсюда
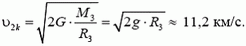
(g = 9,8 м/с2 — ускорение свободного падения у поверхности Земли).
Задача 3. Искусственный Спутник, используемый в системе телесвязи, запущен в плоскости земного экватора так, что все время находится в зените одной и той же точки земного шара. Во сколько раз радиус R орбиты спутника больше радиуса Земли R3 = 6400 км? Ускорение свободного падения у поверхности Земли g = 9,8 м/с2.
По условию задачи спутник все время находится в зените одной и той же точки земного шара. Следовательно, спутник движется по круговой орбите радиусом R с постоянной угловой скоростью, причем его угловая скорость ω равна угловой скорости вращения Земли ω3.
На спутник массой m действует одна сила тяжести 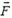 , ее модуль
, ее модуль
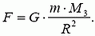
Эта сила и сообщает центростремительное ускорение спутнику:
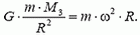
Отсюда найдем ω2:
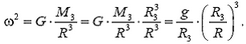
С другой стороны,
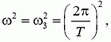
где T — период обращения Земли вокруг собственной оси (сутки).
Приравнивая два последних выражения, получим
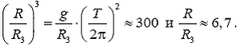
Задача 4. Космонавты, высадившиеся на Луну, должны возвратиться на базовый космический корабль, который летает по круговой орбите на высоте, равной радиусу Луны Rл = 1740 км. Какую начальную скорость на поверхности Луны необходимо сообщить лунной кабине, чтобы стыковка с базовым кораблем стала возможной без дополнительной коррекции величины скорости кабины? Ускорение свободного падения на поверхности Луны gл = 1,7 м/с2.
Запишем уравнение движения космического корабля:
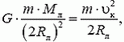
где m — месса корабля, Mл — масса Луны, υк — линейная скорость движения корабля по круговой орбите. Из этого уравнения найдем
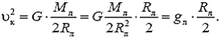
Для того чтобы стыковка лунной кабины с базовым кораблем произошла без дополнительной коррекции, скорость кабины в момент сближения с кораблем должна быть равна по модулю скорости корабля υк.
Связь между начальной скоростью кабины υ на поверхности Луны и ее скорость υк на орбите корабля можно найти из закона сохранения полной энергии кабины:
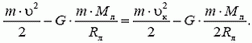
Подставляя в это уравнение выражение для 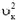 , получим
, получим
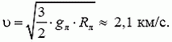
Упражнения
1. Спутник массой M = 200 кг движется по круговой орбите вокруг Земли. Его расстояние от поверхности Земли мало по сравнению с радиусом Земли. На сколько можно изменить это расстояние, если из спутника произвести выстрел? Масса пули m = 5 г. ее скорость υ = 1 км/с. Стреляют в направлении, противоположном полету спутника.
2. Один из спутников Юпитера движется по орбите радиусом R1 = 4,22·105 км и совершает полный оборот за время T1 = 1,77 дня. Во сколько раз масса Юпитера больше массы Земли? Известно, что Луна движется по орбите радиусом R1 = 3,8·105 км с периодом T2 = 27,3 дня.
3. На какое максимальное расстояние от Солнца удаляется комета Галлея? Период обращения ее вокруг Солнца равен T = 76 годам минимальное расстояние кометы от Солнца равно rmin = 1,8·108 км. Радиус орбиты Земли равен R = 1,5·108 км.
4. Искусственный спутник вращается вокруг Земли по круговой орбите радиусом R. Какую минимальную дополнительную скорость u необходимо сообщить спутнику, чтобы он ушел из зоны притяжения Земли (на бесконечность)?
Ответы
1. 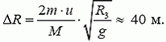 Указание. Изменение скорости спутника Δυ и изменение радиуса его орбиты ΔR связаны соотношением 2υ·Δυ = g·ΔR.
Указание. Изменение скорости спутника Δυ и изменение радиуса его орбиты ΔR связаны соотношением 2υ·Δυ = g·ΔR.
2. 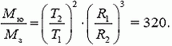
3. 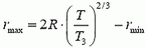 = 52·108 км, где T3 = 1 год — период обращения Земли вокруг Солнца. Указание. Воспользуйтесь первым и третьим законами Кеплера.
= 52·108 км, где T3 = 1 год — период обращения Земли вокруг Солнца. Указание. Воспользуйтесь первым и третьим законами Кеплера.
4. 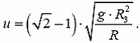
| Выложил | alsak |
| Опубликовано | 02.03.09 |
| Просмотров | 18878 |
| Рубрика | Решение задач |
| Тема | Динамика Законы сохранения |