Баканина Л.П. Закон сохранения импульса при соударениях // Квант
Баканина Л. Закон сохранения импульса при соударениях // Квант. – 1977. – № 3. – С. 46-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Закон сохранения импульса (количества движения) выполняется для замкнутых систем, то есть таких, которые включают в себя все взаимодействующие тела, так что ни на одно из тел системы не действуют внешние силы. Однако при решении многих физических задач оказывается, что импульс может оставаться постоянным и для незамкнутых систем. Правда, в этом случае количество движения сохраняется лишь приближенно. Попытаемся разобраться, в чем тут дело.
Изменение импульса 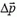 незамкнутой системы равно суммарному импульсу внешних сил. Обозначим через
незамкнутой системы равно суммарному импульсу внешних сил. Обозначим через 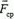 среднее значение результирующей внешней силы, действующей на систему в течение промежутка времени Δt. Тогда
среднее значение результирующей внешней силы, действующей на систему в течение промежутка времени Δt. Тогда
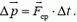
Если абсолютная величина этой силы не слишком велика и время, в течение которого действует сила, мало, то произведение 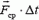 тоже будет малым. В таком случае возникает необходимость оценки, с какой точностью можно считать импульс системы неизменным.
тоже будет малым. В таком случае возникает необходимость оценки, с какой точностью можно считать импульс системы неизменным.
Кроме того, не следует забывать, что импульс — вектор, и, следовательно, можно говорить о сохранении проекции этого вектора на какое-либо направление. Действительно, если система не замкнута, но внешние силы таковы, что сумма проекций всех сил на некоторое направление равна нулю, то проекция импульса системы на это направление остается величиной постоянной. Незамкнутая система в этом направлении аналогична замкнутой.
Кратковременные взаимодействия возникают, например, при взрывах, выстрелах, соударениях. Такого типа задачи мы и обсудим. Постараемся в каждом конкретном случае выяснить, выполняется или не выполняется закон сохранения импульса и от чего это зависит.
Задача 1. Из пушки, соскальзывающей без трения по наклонной плоскости и прошедшей уже путь l, производится выстрел в горизонтальном направлении (рис. 1). При какой скорости снаряда пушка остановится после выстрела? Масса снаряда m много меньше массы пушки M, угол наклона плоскости α.
Перед выстрелом пушка (вместе со снарядом), прошедшая путь l, имеет импульс 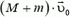 , направленный вдоль наклонной плоскости. Модуль этого импульса можно найти из закона сохранения энергии:
, направленный вдоль наклонной плоскости. Модуль этого импульса можно найти из закона сохранения энергии:
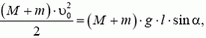
и
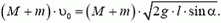
Сразу после выстрела пушка остановилась, а снаряд полетел в горизонтальном направлении. Таким образом, несмотря на кратковременность взаимодействия пушки и снаряда, импульс этой системы не сохраняется. Почему же?
Во время выстрела резко возрастает сила давления пушки на наклонную плоскость, а значит, возрастает и сила реакции со стороны плоскости, так что импульс этой силы оказывается достаточно большим. Он то и изменяет суммарный импульс пушки и снаряда.
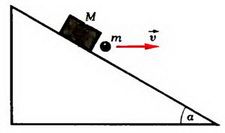
Рис. 1.
Однако в направлении вдоль наклонной плоскости проекция силы реакции равна нулю, а проекция импульса силы тяжести 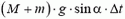 за малое время выстрела Δt мала и при выстреле не увеличивается. Поэтому можно, с некоторой степенью точности, считать, что в направлении вдоль наклонной плоскости проекция количества движения системы пушка — снаряд сохраняется. Следовательно, проекция суммарного импульса пушки и снаряда до выстрела равна проекции снаряда после выстрела (пушка покоится):
за малое время выстрела Δt мала и при выстреле не увеличивается. Поэтому можно, с некоторой степенью точности, считать, что в направлении вдоль наклонной плоскости проекция количества движения системы пушка — снаряд сохраняется. Следовательно, проекция суммарного импульса пушки и снаряда до выстрела равна проекции снаряда после выстрела (пушка покоится):

Отсюда модуль скорости снаряда непосредственно после выстрела
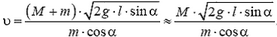
При решении этой задачи мы полагали, что в направлении вдоль наклонной плоскости система пушка — снаряд ведет себя как замкнутая система. Однако оценить, с какой степенью точности это справедливо, мы не можем, так как система взаимодействующих тел сложная и нет необходимых данных для такой оценки.
Разберем теперь две задачи с более простым взаимодействием, где такую оценку можно сделать.
Задача 2. В деревянный шар массы M = 1 кг, падающий вниз со скоростью V0 = 1 м/c, стреляют снизу из ружья и пробивают его насквозь. Какую скорость будет иметь шар сразу после этого? Скорость пули υ0 = 300 м/с, после вылета из шара υ = 100 м/с, масса пули m = 10 г.
Оценим, с какой точностью можно считать систему шар — пуля замкнутой во время их взаимодействия. Другими словами, выясним, можно ли пренебречь импульсом силы тяжести за это время.
Время взаимодействия 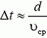 , где d — диаметр шара, a υср — средняя скорость пули внутри шара. Диаметр шара можно оценить, зная, что плотность дерева ρ приблизительно равна плотности воды ρв = 103 кг/м3:
, где d — диаметр шара, a υср — средняя скорость пули внутри шара. Диаметр шара можно оценить, зная, что плотность дерева ρ приблизительно равна плотности воды ρв = 103 кг/м3:
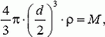
и
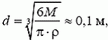
а
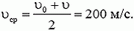
Таким образом, Δt ≈ 5·10–4 c. Импульс силы тяжести системы за это время (а значит, и изменение суммарного импульса шара и пули)
p = (M + m)·g·Δt ≈ 5·10–3 Н·с.
Количество движения системы перед взаимодействием
p0 = m·υ0 – M·V0 = 2 Н·с.
Тогда отношение
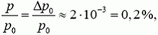
и, следовательно, с точностью до 0,2 % можно считать, что во время взаимодействия импульс системы не изменяется.
Запишем закон сохранения для проекции импульса на ось, направленную вертикально вверх:
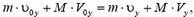
или
m·υ0 – M·V0 = m·υ+ M·Vy.
Отсюда проекция скорости шара после взаимодействия
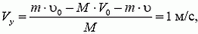
то есть шар начнет двигаться вверх со скоростью 1 м/сек.
Задача 3. Шарик бросают вертикально вверх со скоростью υ0 = 1 м/с. Когда он достиг верхней точки своего подъема, бросают еще такой же шарик с начальной скоростью 2υ0. Определить скорости шариков после столкновения, если столкновение можно считать абсолютно упругим.
Аналогично предыдущей задаче прежде всего оценим, с какой степенью точности систему двух шариков во время соударения можно считать замкнутой. Для этого найдем импульс системы до удара, импульс силы тяжести за время удара и сравним их между собой.
Пусть шарики столкнулись на высоте h через время t после начала движения второго шарика (рис. 2). Тогда для первого шарика
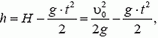
где 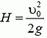 — максимальная высота подъема. Для второго шарика
— максимальная высота подъема. Для второго шарика
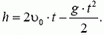
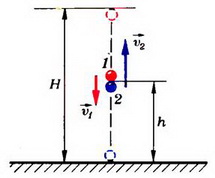
Рис. 2.
Отсюда 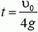 , и скорости обоих шариков непосредственно перед столкновением равны
, и скорости обоих шариков непосредственно перед столкновением равны
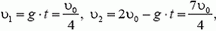
причем первый шарик движется вниз, а второй — вверх.
Итак, количество движения системы до взаимодействия
p0 = m·υ2 – m·υ1 = 1,5m·υ0.
Теперь попытаемся оценить время взаимодействия и импульс силы тяжести за это время. Для этого мы должны представить себе, как происходит процесс соударения. Рассмотрим вначале соударение торцами двух одинаковых стержней. При ударе в торце возникает упругая деформация, которая распространяется вдоль стержня, то есть в стержне возникает звуковая волна. Дойдя до противоположного конца стержня, волна отражается и возвращается обратно. Можно сказать, что на этом процесс соударения заканчивается, и время взаимодействия стержней равно времени прохождения звуковой волны вдоль стержня и обратно. На самом деле картина взаимодействия гораздо сложнее, а в случае шариков, где возникающая упругая волна не плоская, — тем более. Однако для оценки и здесь будем считать, что с точностью до порядка величины время соударения равно времени распространения звуковой волны внутри шарика: 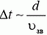 . Скорость звука в твердых телах порядка нескольких километров в секунду. Если диаметр шарика порядка сантиметра, то Δt ~ 10–5 c, и импульс силы тяжести
. Скорость звука в твердых телах порядка нескольких километров в секунду. Если диаметр шарика порядка сантиметра, то Δt ~ 10–5 c, и импульс силы тяжести 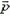 по абсолютной величине во много раз меньше импульса шариков до взаимодействия:
по абсолютной величине во много раз меньше импульса шариков до взаимодействия:
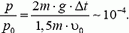
Таким образом, и в этом случае мы можем считать систему соударяющихся шариков замкнутой. (Конечно, дальнейшее движение шариков существенно зависит от силы тяжести.) Так как удар шариков абсолютно упругий, воспользуемся законами сохранения механической энергии и проекции импульса на ось, направленную вертикально вверх:
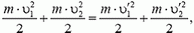
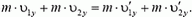
Подставив сюда соответствующие значения для υ1 и υ2:
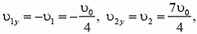
найдем
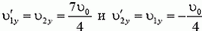
— при упругом ударе шарики равных масс обмениваются скоростями.
Не следует, однако, думать, что всегда при соударениях можно пренебречь действием внешних сил и считать систему замкнутой. Для примера рассмотрим такую задачу.
Задача 4. Мешок с мукой сползает без начальной скорости с высоты Н по гладкой доске, наклоненной подуглим α = 60° к горизонту. После спуска мешок попадает на горизонтальный шероховатый пол. Коэффициент трения мешка о пол μ = 0,7. Где остановится мешок?
После спуска с доски мешок имеет скорость 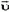 , направленную вдоль доски (рис. 3). Ее абсолютную величину можно найти из закона сохранения механической энергии, так как доска гладкая и потерь энергии нет:
, направленную вдоль доски (рис. 3). Ее абсолютную величину можно найти из закона сохранения механической энергии, так как доска гладкая и потерь энергии нет:
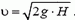
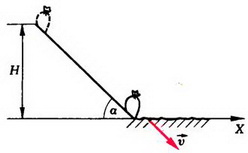
Рис. 3.
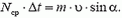
В горизонтальном направлении на мешок действует сила трения скольжения, модуль которой 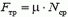 . Импульс этой силы за время удара равен
. Импульс этой силы за время удара равен
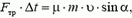
то есть не зависит ни от того, но какому закону изменяется сила реакции опоры (aзначит, и сила давлении мешка на пол), ни от времени соударения. Найдем изменение горизонтальной проекции импульса мешка. Направим ось X по горизонтали вправо, тогда, согласно второму закону Ньютона,
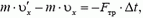
или
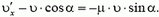
Отсюда проекция скорости, с которой мешок начнет двигаться по полу,
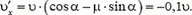
Что означает знак «минус»? Формально знак «минус» говорит о том, что после удара мешок должен двигаться влево, или, другими словами, что импульс силы трения оказался больше первоначальной горизонтальной проекции импульса мешка. Значит, в какой-то момент в процессе соударения проекция скорости мешка на ось Х обратилась в нуль. Начиная с этого момента, наше решение становится неверным. Действительно, модуль силы трения равен μ·Ncp только при скольжении, а в состоянии покоя сила трения может принимать любые значения от 0 до μ·Ncp в зависимости от того, какие силы (кроме силы трения) действуют на тело. В нашем случае никакие другие силы не имеют проекций в горизонтальном направлении, следовательно, в тот момент, когда горизонтальная проекция скорости мешка обратилась в нуль, сила трения тоже обращается в нуль. Таким образом, мешок по полу вообще двигаться не будет.
Наконец, обсудим еще одну достаточно известную задачу на соударение тел. При решении этой задачи обычно используют довольно грубые приближения, никак не оговаривая при этом ни то, что это приближение, ни при каких условиях им можно пользоваться.
Задача 5. На стоящий на гладкой горизонтальной поверхности клин массы М с высоты h падает шар массы m и отскакивает в горизонтальном направлении (рис. 4). Найти горизонтальную проекцию скорости клина 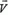 после удара. Трением пренебречь, удар считать абсолютно упругим.
после удара. Трением пренебречь, удар считать абсолютно упругим.
В отличие от всех предыдущих задач здесь нужно рассматривать соударение не двух, а трех тел — шарика, клина и горизонтальной плоскости. В общем случае, не делая никаких дополнительных предположений о механизме удара, решить эту задачу нельзя. В наиболее распространенном решении этой задачи неявно (без всяких оговорок) предполагается, что соударения шарика с клином и клина с горизонтальной плоскостью происходят одновременно, а клин после соударения имеет только горизонтальную проекцию скорости. Затем записываются уравнения законов сохранения механической энергии и импульса:
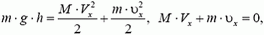
где Vx и υx — соответственно проекции скоростей клина и шарика на горизонтальную ось, направленную вправо. Отсюда
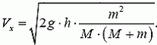
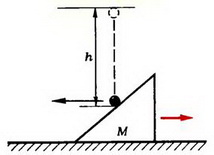
Рис. 4.
Однако в таком решении совершенно не ясно, куда делась вертикальная проекция импульса шарика. Ведь если соударение абсолютно упругое, вертикальная проекция импульса системы не исчезает, а лишь меняет знак! Шарик после удара отскакивает в горизонтальном направлении, плоскость вообще неподвижна. Значит, клин после удара обязательно должен подпрыгнуть. А энергия, связанная с этим движением, в приведенном решении не учитывается.
Физической картине удара больше соответствует предположение о том, что вначале шарик соударяется только с клином, а потом клин, получивший некоторую скорость в результате этого соударения, взаимодействует с горизонтальной плоскостью. После первого соударения вертикальная проекция скорости клина
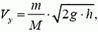
а горизонтальные проекции скоростей клина и шарика, как и в первом решении, связаны соотношением
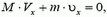 или
или 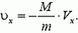
Тогда закон сохранения энергии можно записать в виде
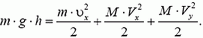
Подставив сюда соответствующие выражения для υx и Vy, найдем горизонтальную проекцию скорости клина:
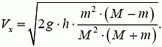
Таким образом, задачу о соударении трех тел мы свели к задаче двух последовательных попарных соударений (второе соударение для решения задачи нам не понадобилось). При этом мы считали, что клин после соударения с шариком движется чисто поступательно. Это может быть только в том случае, если сила давления шарика 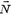 во время удара проходит через центр тяжести О клина (рис. 5).
во время удара проходит через центр тяжести О клина (рис. 5).
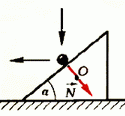
Рис. 5.
Кроме того, заметим, что для того чтобы шарик после соударения отскочил горизонтально, угол клина α должен иметь вполне определенную величину, зависящую от масс шарика и клина.
В заключение предлагаем несколько задач для самостоятельного решения.
Упражнения
1. В центр шара массы m1 = 300 г, лежащего на краю стола, попадает горизонтально летящая пуля массы m2 = 10 г и пробивает его насквозь. Шар падает на пол на расстоянии s1 = 6 м от стола, а пуля — на расстоянии s2 = 15 м. Высота стола H = 1 м. Определить первоначальную скорость пули.
2. Две частицы с массами m и 2m, имеющие импульсы 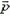 и
и 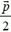 , движутся по взаимно перпендикулярным направлениям. После соударения частицы обмениваются импульсами (рис. 6). Определить выделившееся при ударе количество теплоты.
, движутся по взаимно перпендикулярным направлениям. После соударения частицы обмениваются импульсами (рис. 6). Определить выделившееся при ударе количество теплоты.
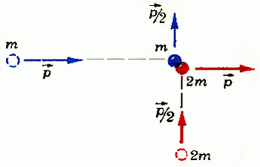
Рис. 6.
3. Мешок с мукой сползает без начальной скорости с высоты Н = 2 м по доске, наклоненной под углом α= 45° к горизонту. После спуска мешок попадает на горизонтальную поверхность. Коэффициент трения мешка о доску и горизонтальную поверхность μ = 0,5. На каком расстоянии от конца доски остановится мешок?
Ответы
1. 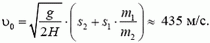
2. 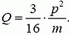
3.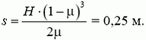
| Выложил | alsak |
| Опубликовано | 09.04.09 |
| Просмотров | 26198 |
| Рубрика | Решение задач |
| Тема | Законы сохранения |